По условию, нужно найти сумму несократимых дробей вида , это означает, что числа и 1001 - взаимно простые.
Разложим число 1001 на простые множители:
Рассмотрим искомую сумму, без учета условия о несократимости дроби . Тогда получим:
Задача сводится к нахождению суммы . Но мы помним, что на самом деле нас интересует сумма только тех чисел от 1 до 2002, которые являются взаимно простыми с числом 1001.
Найдем количество чисел от 1 до 2002, которые не являются взаимно простыми с числом 1001. По отношению к делимости на делители числа 1001, то есть на 7, 11, 13 все такие числа можно разделить на несколько групп:
- делятся на 7, но не делятся на 11, 13;
- делятся на 11, но не делятся на 7, 13;
- делятся на 13, но не делятся на 7, 11;
- делятся на 7, 11, но не делятся на 13;
- делятся на 7, 13, но не делятся на 11;
- делятся на 11, 13, но не делятся на 7;
- делятся на 7, 11, 13.
Количества таких чисел соответственно равно:
Найти итоговое количество чисел, не взаимно простых с 1001 можно по формуле включений-исключений, которая запишется в виде:
Формула подразумевает, что числа, имеющие два делителя из набора (7, 11, 13) были посчитаны среди первых трех слагаемых дважды, поэтому их необходимо один раз отнять. В свою очередь числа, делящиеся на каждое число набора (7, 11, 13) были посчитаны 3 раза со знаком "плюс" и 3 раза со знаком "минус", поэтому их необходимо отдельно прибавить.
Тогда, количество чисел, взаимно простых с 1001:
Составим следующую конструкцию. запишем числа от 1 до 2002 в столбик, а точнее для дальнейшего удобства - от 0 до 2002:
Во второй столбик запишем те же самые числа в обратном порядке:
Заметим, что сумма чисел в каждой строчке равна 2002.
Нетрудно понять, что два числа в одной строчке либо оба делятся на 7 (аналогично, на 11, на 13), либо оба не делятся. Поскольку 2002 делится на 7, то делимость первого числа в строчке гарантирует делимость второго числа и наоборот.
Тогда, вычеркнем из нашей таблицы 562 строчки, в которых первое число (а значит и второе тоже) не является взаимно простым с числом 1001. Вычеркнем также первую вс строчку (0-2002).
В таблице останется как было определено ранее 1440 чисел в каждом из столбцов. Поскольку мы знаем суммы чисел в каждой строчке, то легко определяется сумма всех чисел в таблице:
Заметим, что в таблице записан двойной набор тех чисел, что нам нужно сложить в числителе искомой величины.
Найдем последний 30-й член прогрессии по формуле an=a1+d(n-1):
а30=16+2*29=84
Т.к. максимальный член больше 70, то в этой прогрессии встретим числа 38 и 70, но не встретим 53, т.к. разность прогрессии - четное число и первый член прогрессии - четное число.
Найдем, какими по порядку членами являются числа 38 и 70 (из формул выше).
По условию, нужно найти сумму несократимых дробей вида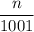 , это означает, что числа
, это означает, что числа 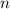 и 1001 - взаимно простые.
и 1001 - взаимно простые.
Разложим число 1001 на простые множители:
Рассмотрим искомую сумму, без учета условия о несократимости дроби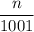 . Тогда получим:
. Тогда получим:
Задача сводится к нахождению суммы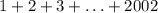 . Но мы помним, что на самом деле нас интересует сумма только тех чисел от 1 до 2002, которые являются взаимно простыми с числом 1001.
. Но мы помним, что на самом деле нас интересует сумма только тех чисел от 1 до 2002, которые являются взаимно простыми с числом 1001.
Найдем количество чисел от 1 до 2002, которые не являются взаимно простыми с числом 1001. По отношению к делимости на делители числа 1001, то есть на 7, 11, 13 все такие числа можно разделить на несколько групп:
- делятся на 7, но не делятся на 11, 13;
- делятся на 11, но не делятся на 7, 13;
- делятся на 13, но не делятся на 7, 11;
- делятся на 7, 11, но не делятся на 13;
- делятся на 7, 13, но не делятся на 11;
- делятся на 11, 13, но не делятся на 7;
- делятся на 7, 11, 13.
Количества таких чисел соответственно равно:
Найти итоговое количество чисел, не взаимно простых с 1001 можно по формуле включений-исключений, которая запишется в виде:
Формула подразумевает, что числа, имеющие два делителя из набора (7, 11, 13) были посчитаны среди первых трех слагаемых дважды, поэтому их необходимо один раз отнять. В свою очередь числа, делящиеся на каждое число набора (7, 11, 13) были посчитаны 3 раза со знаком "плюс" и 3 раза со знаком "минус", поэтому их необходимо отдельно прибавить.
Тогда, количество чисел, взаимно простых с 1001:
Составим следующую конструкцию. запишем числа от 1 до 2002 в столбик, а точнее для дальнейшего удобства - от 0 до 2002:
Во второй столбик запишем те же самые числа в обратном порядке:
Заметим, что сумма чисел в каждой строчке равна 2002.
Нетрудно понять, что два числа в одной строчке либо оба делятся на 7 (аналогично, на 11, на 13), либо оба не делятся. Поскольку 2002 делится на 7, то делимость первого числа в строчке гарантирует делимость второго числа и наоборот.
Тогда, вычеркнем из нашей таблицы 562 строчки, в которых первое число (а значит и второе тоже) не является взаимно простым с числом 1001. Вычеркнем также первую вс строчку (0-2002).
В таблице останется как было определено ранее 1440 чисел в каждом из столбцов. Поскольку мы знаем суммы чисел в каждой строчке, то легко определяется сумма всех чисел в таблице:
Заметим, что в таблице записан двойной набор тех чисел, что нам нужно сложить в числителе искомой величины.
Тогда:
ответ: 1440
d=18-16=2
Найдем последний 30-й член прогрессии по формуле an=a1+d(n-1):
а30=16+2*29=84
Т.к. максимальный член больше 70, то в этой прогрессии встретим числа 38 и 70, но не встретим 53, т.к. разность прогрессии - четное число и первый член прогрессии - четное число.
Найдем, какими по порядку членами являются числа 38 и 70 (из формул выше).
16+2(n-1)=38
2n-2=38-16=22
2n=22+2=24
n=12, т.е. число 38 - 12-й член прогрессии
16+2(n-1)=70
2n-2=70-16=54
2n=54+2=56
n=28, т.е. число 70 - 28-й член прогрессии