Пусть длина участка равна х м., а ширина - у м. Зная, что периметр = 160 м, а формула для нахождения периметра P=2*(a+b) и площадь участка = 1596 м^2 а формула S=a*b, составим систему уравнений:
Выразив одну величину через другую, выполним подстановку и решим уравнение с одним неизвестным, получим :
(80-у)*у=1596
80у-у^2=1596
y^2-80y+1596=0
D=b^2-4ac=80^2-4*1*1596=6400-6384=16 D>0, уравнение имеет 2 корня:
у1,2=(-b±√D)/2a
y1=(80-)/2*1=(80-4)/2=76/2=38
y2=(80+)/2*1=(80+4)/2=84/2=42
Тогда х1+38=80
х1=80-38=42
х2+42=80
х2=80-42=38. Значит размеры садового участка равны 38 м и 42 м, меньший из них равен 38 м
Прямоугольный треугольник с катетами 3 и 4 - египетский, его гипотенуза 5 ( проверьте по т.Пифагора).
Проекция ВС наклонной В1С перпендикулярна СА. По т. о 3-х перпендикулярах В1С⊥СА. Треугольник В1СА - прямоугольный с углом В1АС=60°. В1С=АС•tg60°=4√3. Т.к. призма прямая, боковые ребра перпендикулярны основаниям, поэтому треугольник В1ВС прямоугольный. По т. Пифагора В1В=√(B1C²-BC²)=√[(4√3)²-3²]=√39
Боковое ребро прямой призмы является её высотой, а её боковые грани - прямоугольники.
Площадь боковой поверхности призмы находят умножением её высоты на периметр основания.
Объяснение:
Пусть длина участка равна х м., а ширина - у м. Зная, что периметр = 160 м, а формула для нахождения периметра P=2*(a+b) и площадь участка = 1596 м^2 а формула S=a*b, составим систему уравнений:
Выразив одну величину через другую, выполним подстановку и решим уравнение с одним неизвестным, получим :
(80-у)*у=1596
80у-у^2=1596
y^2-80y+1596=0
D=b^2-4ac=80^2-4*1*1596=6400-6384=16 D>0, уравнение имеет 2 корня:
у1,2=(-b±√D)/2a
y1=(80-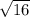
)/2*1=(80-4)/2=76/2=38
y2=(80+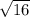
)/2*1=(80+4)/2=84/2=42
Тогда х1+38=80
х1=80-38=42
х2+42=80
х2=80-42=38. Значит размеры садового участка равны 38 м и 42 м, меньший из них равен 38 м
ответ: 12√39 (ед. площади)
Объяснение:
Прямоугольный треугольник с катетами 3 и 4 - египетский, его гипотенуза 5 ( проверьте по т.Пифагора).
Проекция ВС наклонной В1С перпендикулярна СА. По т. о 3-х перпендикулярах В1С⊥СА. Треугольник В1СА - прямоугольный с углом В1АС=60°. В1С=АС•tg60°=4√3. Т.к. призма прямая, боковые ребра перпендикулярны основаниям, поэтому треугольник В1ВС прямоугольный. По т. Пифагора В1В=√(B1C²-BC²)=√[(4√3)²-3²]=√39
Боковое ребро прямой призмы является её высотой, а её боковые грани - прямоугольники.
Площадь боковой поверхности призмы находят умножением её высоты на периметр основания.
S(бок)=В1В•(АВ+ВС+АС)=√39•12=12√39 (ед. площади)