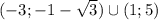Стрела и сердечко расположены так,как показано на рисунке. за один ход стрела сдвигается на три сектора по часовой стрелке и одновременно сердечко на четыре сектора против часовой стрелки. через сколько ходов стрела и сердечко окажутся в каком-то одном секторе? ​

5.

y=-x^2-2x+3,

a=-1<0 - ветви параболы вниз;

x_0=-b/(2a)=-(-2)/(2*(-1))=-1,

y_0=-(-1)^2-2*(-1)+3=4,

(-1;4) - вершина параболы;

x=0, y=3,

(0;3) - пересечение с Оу,

y=0, -x^2-2x+3=0,

x^2+2x-3=0,

по теореме Виета x_1=-3, x_2=1,

(-3;0), (1;0) - пересечения с Оx;

1) E_y=(-∞;4);

2) x∈(-1;+∞);

6.

(х^2+2х+1)(х^2-6х-16)<0,

(х^2+2х+1)(х^2-6х-16)=0,

х^2+2х+1=0, (x+1)^2=0, x+1=0, x=-1;

х^2-6х-16=0, по теореме Виета x_1=-2, x_2=8; х^2-6х-16=(x+2)(x-8);

(x+1)^2(x+2)(x-8)<0,

(x+1)^2≥0, x∈R,

(x+2)(x-8)<0,

-2<x<8,

x∈(-2;8);

7.

x^2-6bx+3b=0,

D<0,

D/4=k^2-ac=(-3b)^2-3b=3b^2-3b=3b(b-1),

3b(b-1)<0,

3b(b-1)=0,

b_1=0, b_2=1,

0<b<1,

b∈(0;1);

8.

ΔABC, уг.C=90°, CE - высота, AE=16см, BE=9см;

AB=AE+BE (по свойству сложения отрезков),

AB=16+9=25см;

AC^2=AB*AE (катет есть среднее геометрическое гипотенузы и смежного сегмента),

AC^2=25*16=400, AC=20см,

BC^2=AB*BE=25*9=225, BC=15см,

P=AB+AC+BC=25+20+15=60см.

ОДЗ:

Решаем каждое неравенство:

   ⇒     ⇒

   ⇒      ⇒      

Подмодульные выражения обращаются в 0 в точках

   и  

Это точки делят числовую прямую на три промежутка.

Раскрываем знак модуля на промежутках:

(-∞;-4]

|x+4|=-x-4

|x|=-x

    ⇒        ⇒    x < 1

решение неравенства (-∞;-4]

(-4;0]

|x+4|=x+4

|x|=-x

    ⇒        ⇒    x < -2 или  x > 1

решение неравенства (-4;-2)

(0;+∞)

|x+4|=x+4

|x|=x

    ⇒        ⇒    x > 1

решение неравенства (1;+∞]

Объединяем  ответы трех случаев:

   при  

ОДЗ:

Решаем неравенство: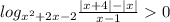  

Два случая:

если основание логарифмической функции >1, то она возрастает и большему значению функции соответствует большее значение аргумента

    ⇒         ⇒          

второе неравенство решаем на промежутках  так:

(-∞;-4]

   ⇒       ⇒      ⇒ (-3;-1)

не принадлежат (-∞;-4]

на (-4;0]

     ⇒          ⇒    x < -5   или  x > 1

не принадлежат (-4;0]

(0;+∞)

     ⇒        ⇒      ⇒

о т в е т  этого случая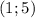

если основание логарифмической функции 0 < a < 1, то она убывает и большему значению функции соответствует меньшее значение аргумента

    ⇒          ⇒  

второе неравенство решаем на промежутках так:

(-∞;-4]

   ⇒       ⇒      ⇒

(-∞;-3)U(1;+∞)

о т в е т. (-∞;-4]

на (-4;0]

     ⇒          ⇒     -5 < x < 1

о т в е т.  (-4;0]

(0;+∞)

     ⇒        ⇒      ⇒

о т в е т  этого случая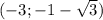

С учетом ОДЗ получаем окончательный ответ: