Студент приготовил к экзамену 50 вопросов из 60. В 30 билетах вопросы распределены случайным образом. Для положительной оценки надо ответить хотя бы на один из двух вопросов билета. Найти вероятность того, что студент сдаст экзамен. С подробным решением задачи
ответ: 43
Объяснение:
Пусть одно из чисел равно
, тогда второе 
.
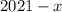Пусть:
Тогда:
Где
и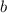 
взаимнопростые натуральные числа. Для определенности будем считать, что 
.
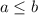Заметим, что числа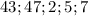
простые. Из второго уравнения очевидно, что 
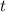не делится на 
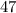, то есть 
.
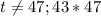Предположим теперь, что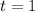
, тогда 
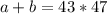, но тогда, поскольку сумма двух чисел делится на 
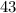, то либо каждое из них делится на 
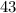, либо не одно из них не делится на 
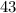. Если каждое из них делится на 
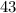, то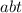 
делится на 
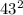, но правая часть второго равенства делится только на первую степень числа 
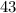. Если же оба из них не делятся на 
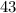, то с учетом того, что 
, 
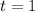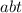не делится на 
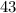. То есть мы пришли к противоречию.
Как видим, остается единственный вариант:
Пусть х1 и х2 - любые действительные числа (из множества R), удовлетворяющие единственному условию х2 > х1
Тогда функция y = f(x) называется:
- убывающей на R, если при этом: f(x2) < f(x1);
- возрастающей на R, если при этом: f(x2) > f(x1).
Объяснение:
Функция возрастающая - если большему аргументу отвечает большее значение фунцкции. Пусть у нас аргументы буду
По условию
1) Если мы умножим неравенство аргументов на -1, получится, что
Поскольку мы использовали те же значения функции (при данных значениях аргумента значения функций начальных и этих будет одинаково), то
Функция будет убывающей
2)
Поэтому функция возрастающая