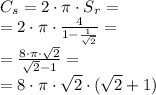Сума потроєного другого і четвертого членів арифметичної прогресії дорівнює 20. Визнач, при якому значенні різниці прогресії добуток третього і п'ятого членів прогресії буде найменший.
Відповідь:
різниця прогресії: d=
У розв'язанні завдання використовувалися формули (запиши відсутні числа):
1. a1=
−
d;
2. f(d)=
+
d+
d2
1) 2sin²x+11sinx+5=0
sinx=t
2t²+11t+5=0
D=121-40=81; 9
t=-11±9/4
t1=-5, t2=-0.5
2) 2sin²x-3sinx-2=0
sinx=t
2t²-3t-2=0
D=9+16=25; 5
t=3±5/4;
t1=-0.5, t2=2
3) 2sin²-7sinx-4=0
sinx=t
2t²-7t-4=0
D=49+32=81; 9
t=7±9/4
t1=-0.5, t2=4
4) 2cos²x+7cosx-4=0
cosx=t
2t²+7t-4=0
D=49+32=81; 9
t=-7±9/4
t1=-4, t2=0.5
5) -8cos²x+4=0
cos²x=t
-8t+4=0
-8t=-4
t=0.5
6) 2cos²x+3cosx-2=0
cosx=t
2t²+3t-2=0
D=9+16=25; 5
t=-3±5/4
t1=-0.5, t2=2
7) 4sin²x+12sinx+5=0
sinx=t
4t²+12t+5=0
D=144-80=64; 8
t=-12±8/8
t1=0.5, t2=1.5
8) 4cos²x+12cosx+5=0
cosx=t
4t²+12t+5=0
D=144-80=64; 8
t=-12±8/8
t1=0.5, t2=1.5
Если вписать квадрат в окуржность, то его диагональ будет диаметром этой окружности (угол опирающийся на диаметр - прямой). Таким образом длина диагонали квадрата вписанного в окружность: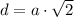
, где a - сторона квадрата. Так как диагональ есть диаметр то она равна двум радиусам: 
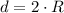. Тогда выразим длину стороны квадрата: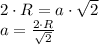 
Если вписать окружность в квадрат, то ее радиус будет равен половине стороны квадрата: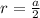
. Подставив предыдущую формулу в данную, получим: 
.
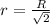Таким образом мы получили бесконечно убывающую геометрическую прогрессию радиусов окружностей. Первый элемент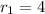
, знаменатель прогресии 
.
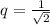Сумма всех радиусов равна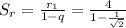
.
Тогда сумма длин всех окружностей: