Сумма членов последовательности чисел представляет собой бесконечно убывающую геометрическую прогрессию со значением 8. Если сумма кубиков членов равна 37/512, то первый член и кратность этой прогрессии находить.
Во втором неравенстве перенесём все члены уравнения в левую часть, приравняем к нулю и решим, как квадратное уравнение:
х-5-4+2х²≤0
2х²+х-9=0
х₁,₂=(-1±√1+72)/4
х₁,₂=(-1±√73)/4
х₁=(-1-√73)/4 ≈ -9,5
х₂=(-1+√73)/4 ≈ 7,5
Начертим СХЕМУ параболы, которую обозначает данное уравнение (ничего вычислять не надо). Просто начертим схематично оси, параболу с ветвями вверх, и отметим на оси Ох точки х₁ ≈ -9,5 и
х₂ ≈ 7,5. Ясно видно, что у<0 при х от -9,5 до 7,5, то есть,
решение второго неравенства х∈[(-1-√73)/4, (-1+√73)/4]
Решим первое неравенство.
3х+4≤4х+6
3х-4х ≤6-4
-х ≤2
х -2 знак меняется
Решение первого неравенства х∈[-2, ∞).
Отметим на числовой оси решение первого неравенства и решение второго, чтобы найти пересечение решений, то есть, такое решение, которое подходит и первому, и второму неравенству.
Решение системы неравенств [-2, (-1+√73)/4] х от -2 до 7,5.
Неравенства нестрогие, скобки квадратные.
2. Решите двойное неравенство -3<2-5х<1
Решается как система:
2-5х>-3
2-5х<1
-5х> -3-2
-5x<1-2
-5x> -5
-5x< -1
x<1 знак меняется x ∈(-∞, 1) решение 1-го неравенства
x>0,2 знак меняется x ∈(0,2, ∞) решение 2-го неравенства
Отметим на числовой оси решение первого неравенства и решение второго, чтобы найти пересечение решений, то есть, такое решение, которое подходит и первому, и второму неравенству.
Значит, нужно найти два последовательных натуральных числа, произведение которых должно быть делимо и на 2 (т. е. одно из них д. б. чётным, что всегда соблюдается) и на 3^5. Если оно из чисел делится на 3, то соседние ему числа не делятся на 3. Следовательно, одно из чисел обязательно должно быть делимо на 3^5= 243. Наименьшее из таких чисел: 243. Рядом с ним есть два числа: 242 и 244. Выбираем меньшее из них: 242. Таким образом, n= 242.
1)Решение системы неравенств [-2, (-1+√73)/4]
2)Решение системы неравенств х∈(0,2, 1)
Объяснение:
1. Решите систему неравенств:
3х+4≤4х+6
х-5≤4-2х²
Во втором неравенстве перенесём все члены уравнения в левую часть, приравняем к нулю и решим, как квадратное уравнение:
х-5-4+2х²≤0
2х²+х-9=0
х₁,₂=(-1±√1+72)/4
х₁,₂=(-1±√73)/4
х₁=(-1-√73)/4 ≈ -9,5
х₂=(-1+√73)/4 ≈ 7,5
Начертим СХЕМУ параболы, которую обозначает данное уравнение (ничего вычислять не надо). Просто начертим схематично оси, параболу с ветвями вверх, и отметим на оси Ох точки х₁ ≈ -9,5 и
х₂ ≈ 7,5. Ясно видно, что у<0 при х от -9,5 до 7,5, то есть,
решение второго неравенства х∈[(-1-√73)/4, (-1+√73)/4]
Решим первое неравенство.
3х+4≤4х+6
3х-4х ≤6-4
-х ≤2
х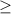
-2 знак меняется
Решение первого неравенства х∈[-2, ∞).
Отметим на числовой оси решение первого неравенства и решение второго, чтобы найти пересечение решений, то есть, такое решение, которое подходит и первому, и второму неравенству.
Решение системы неравенств [-2, (-1+√73)/4] х от -2 до 7,5.
Неравенства нестрогие, скобки квадратные.
2. Решите двойное неравенство -3<2-5х<1
Решается как система:
2-5х>-3
2-5х<1
-5х> -3-2
-5x<1-2
-5x> -5
-5x< -1
x<1 знак меняется x ∈(-∞, 1) решение 1-го неравенства
x>0,2 знак меняется x ∈(0,2, ∞) решение 2-го неравенства
Отметим на числовой оси решение первого неравенства и решение второго, чтобы найти пересечение решений, то есть, такое решение, которое подходит и первому, и второму неравенству.
Решение системы неравенств х∈(0,2, 1)
Неравенства строгие, скобки круглые.
S= n(n+1)/2= 243k= 3^5*k.
n(n+1)= 2*243k= 486k= 2*3^5*k.
Значит, нужно найти два последовательных натуральных числа, произведение которых должно быть делимо и на 2 (т. е. одно из них д. б. чётным, что всегда соблюдается) и на 3^5. Если оно из чисел делится на 3, то соседние ему числа не делятся на 3. Следовательно, одно из чисел обязательно должно быть делимо на 3^5= 243. Наименьшее из таких чисел: 243. Рядом с ним есть два числа: 242 и 244. Выбираем меньшее из них: 242. Таким образом, n= 242.