Пусть x - количество монет в мешке, а значит в сундуке: 3x монет. После того, как из мешка переложили 24 монеты, в сундуке стало: 3x+24, а в мешке x−24. И если в сундуке их стало в 7 раз больше чем в мешке, то имеем: 3x+24=7(x−24).
Ну вот мы и составили уравнение (математическую модель), осталось решить уравнение относительно x и записать ответ.
Решим полученное уравнение: 3x+24=7(x−24). Легко увидеть, что уравнение является линейным (узнать как решаются линейные уравнения можно тут.)
Раскроем скобки в правой части уравнения: 3x+24=7x−7⋅24. Перенесём все слагаемые содержащие переменную в правую часть, а всё что не содержит x в левую, получим: 24+7⋅24=7x−3x. После упрощения получили 192=4x, разделим обе части уравнения на коэффициент при неизвестном, т.е на 4, тогда получим x=48.
За переменную x мы обозначали количество монет в мешке, значит в сундуке в три раза больше т.е 3x.
В мешке 48 В сундуке 144
Объяснение:
Пусть x - количество монет в мешке, а значит в сундуке: 3x монет. После того, как из мешка переложили 24 монеты, в сундуке стало: 3x+24, а в мешке x−24. И если в сундуке их стало в 7 раз больше чем в мешке, то имеем: 3x+24=7(x−24).
Ну вот мы и составили уравнение (математическую модель), осталось решить уравнение относительно x и записать ответ.
Решим полученное уравнение: 3x+24=7(x−24). Легко увидеть, что уравнение является линейным (узнать как решаются линейные уравнения можно тут.)
Раскроем скобки в правой части уравнения: 3x+24=7x−7⋅24. Перенесём все слагаемые содержащие переменную в правую часть, а всё что не содержит x в левую, получим: 24+7⋅24=7x−3x. После упрощения получили 192=4x, разделим обе части уравнения на коэффициент при неизвестном, т.е на 4, тогда получим x=48.
За переменную x мы обозначали количество монет в мешке, значит в сундуке в три раза больше т.е 3x.
Монет в мешке: 48
Монет в сундуке: 48⋅3=144
x₁ = 2 + , y₁ = 2
, y₁ = 2 - 3;
- 3;
x₂ = 2 - , y₂ = - 3 - 2
, y₂ = - 3 - 2 :
:
Объяснение:
{ху - х = 4
{2х - у = 7
Выразим y и подставим во второе уравнение
{xy - x = 4
{-y = 7 - 2x
Уберём минус перед y, помножив выражение на (-1)
{xy - x = 4
{y = 2x - 7
Подставляем полученное выражение вместо y
x * (2x - 7) - x = 4
2x² - 7x - x =4
2x² - 8x - 4 = 0
Получаем квадратное уравнение. Сокращаем коэффиценты, деля обе стороны на 2
x² - 4x - 2 = 0
У нас a = 0. По теореме Виета: x₁ + x₂ = −b; x₁ * x₂ = c;
Но для начала проверим дискриминант
D = b² - 4ac
D = 16 - 4 * 1 * (-2)
D = 16 + 8 = 24
Нет такого натурального числа, которое было бы квадратным корнем из 24, поэтому мы не сможем решить теоремой Виета, и продолжаем решать дискриминантом
x₁,₂ =
x₁ = =
= 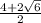 = 2 +
= 2 + 
x₂ =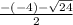 =
= 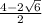 = 2 -
= 2 -
Находим y, подставляя x
2 * (2 + ) - y₁ = 7
) - y₁ = 7
4 + 2 - y₁ = 7
- y₁ = 7
- y₁ = 3 - 2
Убираем минус
y₁ = 2 - 3
- 3
Ищем y₂
2 * (2 - ) - y₂ = 7
) - y₂ = 7
4 - 2 - y₂ = 7
- y₂ = 7
- y₂ = 3 + 2
Снова убираем минус
y₂ = - 3 - 2
ответ: x₁ = 2 + , y₁ = 2
, y₁ = 2 - 3; x₂ = 2 -
- 3; x₂ = 2 - , y₂ = - 3 - 2
, y₂ = - 3 - 2 ;
;