Для решения данной задачи можем построить график функции
, а после найти сколько пересечений имеет данный график с прямой .
Для того график данной функции было проще построить, раскроем модуль |x-2|, имеем.
Изобразим данный два графика, с учетом условий.
1) для построения графика функции нужно сначала построить график функции после сделать следующие преобразования: Выше оси абсцисс(и на самой оси) график функции оставить без изменений, ниже оси абсцисс - симметрия относительно оси абсцисс.
Для построения графика , нужно найти координаты вершины параболы: , найдем корни для того чтобы узнать в каких точках график пересекает оси абсцисс. По теореме Виета (график построен на картинке 1). Теперь сделаем преобразования которые были описаны выше для того чтобы построить модуль этого графика(рис.2). Далее учтем наше ограничение , имеем(рис.3).
2)для построения графика функции нужно сначала построить график функции после сделать следующие преобразования: Выше оси абсцисс(и на самой оси) график функции оставить без изменений, ниже оси абсцисс - симметрия относительно оси абсцисс.
Для построения графика , нужно найти координаты вершины параболы: , найдем корни для того чтобы узнать в каких точках график пересекает оси абсцисс. (график построен на картинке 4). Теперь сделаем преобразования которые были описаны выше для того чтобы построить модуль этого графика(рис.5). Далее учтем наше ограничение , имеем(рис.6).
Теперь объединим построенные два графика для того чтобы получить график функции (рис.7).
Графиком функции является прямая совпадающая (при a=0) или параллельная относительно оси абсцисс. Теперь с графика выясним сколько решений имеет уравнение при различных значениях параметра а(рис.8).
Из рисунка видно что: при нет корней, при два корня, при четыре корня, при три корня, при два корня
ОТВЕТ: при нет корней, при два корня, при четыре корня, при три корня, при два корня
Выбирай любые три:
Переместительный (коммутативный) закон сложения: m + n = n + m . Сумма не меняется от перестановки её слагаемых.
Переместительный (коммутативный) закон умножения: m · n = n · m . Произведение не меняется от перестановки его сомножителей.
Сочетательный (ассоциативный) закон сложения: ( m + n ) + k = m + ( n + k ) = m + n + k . Сумма не зависит от группировки её слагаемых.
Сочетательный (ассоциативный) закон умножения: ( m · n ) · k = m · ( n · k ) = m · n · k . Произведение не зависит от группировки его сомножителей.
Распределительный (дистрибутивный) закон умножения относительно сложения: ( m + n ) · k = m · k + n · k .
Для решения данной задачи можем построить график функции
Для того график данной функции было проще построить, раскроем модуль |x-2|, имеем.
1) для построения графика функции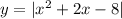 нужно сначала построить график функции
нужно сначала построить график функции 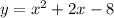 после сделать следующие преобразования: Выше оси абсцисс(и на самой оси) график функции
после сделать следующие преобразования: Выше оси абсцисс(и на самой оси) график функции 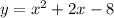 оставить без изменений, ниже оси абсцисс - симметрия относительно оси абсцисс.
оставить без изменений, ниже оси абсцисс - симметрия относительно оси абсцисс.
Для построения графика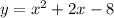 , нужно найти координаты вершины параболы:
, нужно найти координаты вершины параболы: 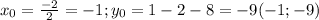 , найдем корни для того чтобы узнать в каких точках график пересекает оси абсцисс. По теореме Виета
, найдем корни для того чтобы узнать в каких точках график пересекает оси абсцисс. По теореме Виета 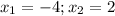 (график построен на картинке 1). Теперь сделаем преобразования которые были описаны выше для того чтобы построить модуль этого графика(рис.2). Далее учтем наше ограничение
(график построен на картинке 1). Теперь сделаем преобразования которые были описаны выше для того чтобы построить модуль этого графика(рис.2). Далее учтем наше ограничение 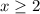 , имеем(рис.3).
, имеем(рис.3).
2)для построения графика функции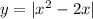 нужно сначала построить график функции
нужно сначала построить график функции 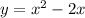 после сделать следующие преобразования: Выше оси абсцисс(и на самой оси) график функции
после сделать следующие преобразования: Выше оси абсцисс(и на самой оси) график функции  оставить без изменений, ниже оси абсцисс - симметрия относительно оси абсцисс.
оставить без изменений, ниже оси абсцисс - симметрия относительно оси абсцисс.
Для построения графика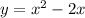 , нужно найти координаты вершины параболы:
, нужно найти координаты вершины параболы: 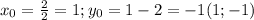 , найдем корни для того чтобы узнать в каких точках график пересекает оси абсцисс.
, найдем корни для того чтобы узнать в каких точках график пересекает оси абсцисс. 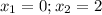 (график построен на картинке 4). Теперь сделаем преобразования которые были описаны выше для того чтобы построить модуль этого графика(рис.5). Далее учтем наше ограничение
(график построен на картинке 4). Теперь сделаем преобразования которые были описаны выше для того чтобы построить модуль этого графика(рис.5). Далее учтем наше ограничение 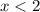 , имеем(рис.6).
, имеем(рис.6).
Теперь объединим построенные два графика для того чтобы получить график функции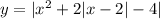 (рис.7).
(рис.7).
Графиком функции является прямая совпадающая (при a=0) или параллельная относительно оси абсцисс. Теперь с графика выясним сколько решений имеет уравнение при различных значениях параметра а(рис.8).
является прямая совпадающая (при a=0) или параллельная относительно оси абсцисс. Теперь с графика выясним сколько решений имеет уравнение при различных значениях параметра а(рис.8).
Из рисунка видно что: при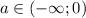 нет корней, при
нет корней, при  два корня, при
два корня, при 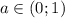 четыре корня, при
четыре корня, при 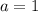 три корня, при
три корня, при 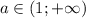 два корня
два корня
ОТВЕТ: при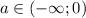 нет корней, при
нет корней, при  два корня, при
два корня, при 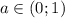 четыре корня, при
четыре корня, при 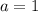 три корня, при
три корня, при 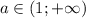 два корня
два корня