Тізбектес бес бүтін санның бастапқы үлеуінің аппараттарының қосындысын қалған екеуінің квадраттарының қосындысымен салыстырыңдар​

Знак сомножителя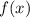 определим непосредственно по графику: выше или ниже оси х располагается график функции.

Знак сомножителя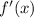 также определим по графику: если функция возрастает, то производная принимает положительные значения, если функция убывает - производная принимает отрицательные значения.

Рассмотрим функцию при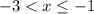 . Функция принимает неположительные значения, значит 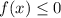. Функция возрастает, значит 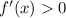. Значит, требуемое неравенство 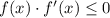выполняется.

Рассмотрим функцию при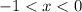 . Функция принимает положительные  значения, значит 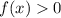. Функция по-прежнему возрастает, значит 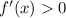. Значит, требуемое неравенство 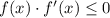не выполняется.

Итак, неравенство среди отрицательных чисел имеет решения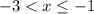 . Наибольшее решение равно -1.

ответ: -1

1) x²-3-4<0;(х-√7)(х+√7)<0;

-√7√7

  +                -                +

х∈(-√7;√7)

второе решение на случай, если при втором коэффициенте потерян х.   x²-3х-4<0; по Виету корни левой части -1 и 4.

-14

   +              -                 +

х∈(-1;4)

2) x²-3x-4>0 уже решил. как второй вариант первого. только здесь другой знак. поэтому ответ х∈(-∞;-2.5)∪(1;+∞)

Решение

x²-3х-4>0; по Виету корни левой части -1 и 4.

-14

   +              -                 +

ответ х∈(-∞;-2.5)∪(1;+∞)

3) 2x²+3x-5>0 , по Виету корни левой части 1 и -2.5

-2.51

+                   -              +

х∈(-∞;-2.5)∪(1;+∞)

4) -6x²+6x+36>0

-6*(x²-x-6)>0; (x²-x-6)<0;

По Виету x=-2; x=3.

-23

  +               -          +

х∈(-2;3)