Числа вида 4n, 4n+1 и 4n+3 представимы в виде разности квадратов: 4n=(n+1)²-(n-1)²; 4n+1=(2n+1)²-(2n)²; 4n+3=(2n+2)²-(2n+1)².
Числа вида 4n+2 не представимы в виде разности квадратов, т.к. иначе 4n+2=a²-b²=(a-b)(a+b). Если а и b имеют разную четность, то а-b и a+b - нечетные числа, и значит (a-b)(a+b) нечетно. Если а и b имеют одинаковую четность, то а-b и a+b - оба четные, и значит (a-b)(a+b) делится на 4. Но число 4n+2 - не является нечетным и не делится на 4. Значит, оно не может быть равно a²-b² ни при каких а и b.
Таким образом, все натуральные числа не представимые в виде разности квадратов имеют вид 4n+2, где n=0,1,2, Так как первое такое число (равное 2) будет при n=0, то трехтысячное число будет при n=2999, т.е. равно 4*2999+2=11998.
Для того чтобы геометрическая прогрессия была бесконечно убывающей, знаменатель геометрической прогрессии должен быть либо меньше 0, но больше -1, либо больше 0, но меньше 1. В таком случае геометрическая прогрессия будет стремиться к 0, но никогда его не достигнет.
Графически это выглядит так: или .
Рассмотрим наши примеры:
1) . Выполняются ли условия неравенства?
. Да, выполняются. Данная геометрическая прогрессия является бесконечно убывающей.
2) . Выполняются ли условия неравенства?
. Да, выполняются. Данная геометрическая прогрессия является бесконечно убывающей.
3) . Выполняются ли условия неравенства?
. Да, выполняются. Данная геометрическая прогрессия является бесконечно убывающей.
4n=(n+1)²-(n-1)²;
4n+1=(2n+1)²-(2n)²;
4n+3=(2n+2)²-(2n+1)².
Числа вида 4n+2 не представимы в виде разности квадратов, т.к. иначе
4n+2=a²-b²=(a-b)(a+b). Если а и b имеют разную четность, то а-b и a+b - нечетные числа, и значит (a-b)(a+b) нечетно. Если а и b имеют одинаковую четность, то
а-b и a+b - оба четные, и значит (a-b)(a+b) делится на 4. Но число 4n+2 - не является нечетным и не делится на 4. Значит, оно не может быть равно a²-b² ни при каких а и b.
Таким образом, все натуральные числа не представимые в виде разности квадратов имеют вид 4n+2, где n=0,1,2, Так как первое такое число (равное 2) будет при n=0, то трехтысячное число будет при n=2999, т.е. равно 4*2999+2=11998.
Для того чтобы геометрическая прогрессия была бесконечно убывающей, знаменатель геометрической прогрессии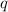 должен быть либо меньше 0, но больше -1, либо больше 0, но меньше 1. В таком случае геометрическая прогрессия будет стремиться к 0, но никогда его не достигнет.
должен быть либо меньше 0, но больше -1, либо больше 0, но меньше 1. В таком случае геометрическая прогрессия будет стремиться к 0, но никогда его не достигнет.
Графически это выглядит так: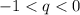 или
или 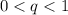 .
.
Рассмотрим наши примеры:
1)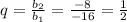 . Выполняются ли условия неравенства?
. Выполняются ли условия неравенства?
2)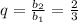 . Выполняются ли условия неравенства?
. Выполняются ли условия неравенства?
3)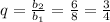 . Выполняются ли условия неравенства?
. Выполняются ли условия неравенства?