Тело движется по прямой так, что расстояние s до него от некоторой точки a этой прямой изменяется по закону 1) s=t^3-4t-8(м),где t-время движения в секундах. найдите скорость тела через 5 с после начала движения 2)t^3+4t+9(м) через 3 с после начала движения

Показать ответ

Ответ:

иаешшвеэщк

26.08.2020 06:57

#1. |2x-3|=3-2x, если х<3/2; |2x-3|=2x-3, если х≥3/2;

|x-2|=2-x, если х<2; |x-2|=-2x, если х≥2;

|x-6|=6-x, если х<6; |x-6|=x-6, если х≥6.

Получаем три случая:

1) на множестве (-∞;3/2)U[2;6) получаем неравенство

(2х-3)(х-2)≥(6-х)+2

2х²-3х-4х+6-6+х-2≥0

2х²-6х-2≥0

х²-3х-1≥0

D=9+4=13

$(x-\frac{3-\sqrt{13}}{2})(x-\frac{3+\sqrt{13}}{2})\geq0 \\\ x \in (-\infty; \frac{3-\sqrt{13}}{2}] \cup [\frac{3+\sqrt{13}}{2}; +\infty)$

C учётом (-∞;3/2)U[2;6) получим $x \in (-\infty; \frac{3-\sqrt{13}}{2}]$

2) на интервале 1,5≤х<2 получим неравенство

(2х-3)(2-х)≥(6-х)+2

4х-6-2х²+3х-6+х-2≥0

-2х²+8х-14≥0

х²-4х+7≤0

D=16-28<0

решений нет

3) на интервале х≥6 получим неравенство

(2х-3)(х-2)≥(х-6)+2

2х²-3х-4х+6+6-х-2≥0

2х²-8х+10≥0

х²-4х+5≥0

D=16-20<0

решений нет

ответ: $x \in (-\infty; \frac{3-\sqrt{13}}{2}]$

#2. Пусть ∆АВС-прямоугольный треугольник с гипотенузой АВ, катетами АС и ВС.

По условию ВС+АВ=11, tg В = 3/4.

По определению тангенса острого угла прямоугольного треугольника

tg B=AC/BC=3/4 => 3BC=4AC =>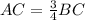 $AC=\frac{3}{4}BC$

По теореме Пифагора АВ² = АС² + ВС²

Пусть ВС=х, тогда АВ=11-х, АС=3х/4

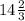
$(11-x)^2=(\frac{3}{4}x)^2+x^2 \\\ 121-22x+x^2=\frac{9}{16}x^2+x^2 \\\ \frac{9}{16}x^2+22x-121=0 \\\ 9x^2+352x-1936=0\\\ \frac{D}{4}=176^2+9*1936=30976+17424=48400 \\\ x_1=-44,\ x_2=\frac{44}{9}=4\frac{8}{9} \\\ BC=4\frac{8}{9} \\\ AC=\frac{3}{4}*\frac{44}{9}=\frac{11}{3}=3\frac{2}{3}\\\ P_{ABC}=AB+BC+AC=11+AC=11+3\frac{2}{3}=14\frac{2}{3}$

ответ: $14\frac{2}{3}$

0,0(0 оценок)

Ответ:

volechka1

07.05.2022 11:22

График линейной функции строится на системе координат. Линейная функция-это прямая, которая обычно дается в виде формулы:
y=kx+m
где x- независимая переменная, её обычно называют аргумент, а y-функция, k и m-некоторые числа.
Например:
(y=kx+m) y=2x+5.
Так как здесь выражена переменная y (y=...) мы можем взять и придумать любую переменную x. Например 2, 3, 0, 5 и т.д. но так как графики у нас не на всю страницу, берем то, что удобнее (чем меньше, тем лучше)
Пример: мы "придумали" что у нас переменная x будет 0. подставляем ее в линейную функцию. Получается:
y=2*0+5. так как если мы что-то умножаем на 0 получится 0, мы смотрим: y=5. то есть: 5=2*0+5. так как решением линейной функции всегда являются две каких-либо точки, мы так и записываем: (0;5)
Это ПЕРВАЯ точка. Для решения функции нам нужны две точки, и мы делаем тоже самое, только берем, естесственно, уже другой x. запишу кратко, как у нас вышла первая точка:
y=2x+5 (мы подставляли: x=0)
y=2*0+5
y=5
ответ: (0;5)
Находим вторую точку, снова "придумываем" x Например: x=1. Подставляем:
y=2x+5
y=2*1+5
y=7
ответ: (1;7)
У нас есть две точки: (0;5) и (1;7), отмечаем их на графике, и проводим ПРЯМУЮ. то есть, на графике мы должны это показать(немного заходим за точки)
Это-график линейной функции

0,0(0 оценок)

Популярные вопросы: Алгебра