Объяснение:
у=х²+4х-2
Это парабола ,ветви вверх. Координаты вершины
а)х₀=-в/2а, х₀=(-4)/2=-2 , у₀=(-2)²+4*(-2)-2=-6 , (-2; -6).
б) во всех четвертях.
с) х=-2
d)Точки пересечения с осью ох, т.е у=0
х²+4х-2=0
Д=в²-4ас, Д=4²-4*4*(-2)=16+32=48=16*3
х₁=(-в+√Д):2а , х₁=(-4+4√3):2 , х₁=2(-2+2√3):2 , х₁=-2+2√3, (-2+2√3;0)
х₂=(-в-√Д):2а , х₂=(-4-4√3):2 , х₂=2(-2-2√3):2 , х₂=-2-2√3 , (-2-2√3;0)
Точки пересечения с осью оу, т.е. х=0, у=-2 (0;-2)
Доп.точки у=х²+4х-2 :
х: -5 -4 -3 1
у: 3 -2 -5 3
2)у=-х²-2х+6 Это парабола ,ветви вниз.
а)f(2)=-(2)²-2*2+6=-4-4+6=-2,
f(-2)=-(-2)²-2*(-2)+6=-4+4+6=6,
б) точка (-3;к) принадлежит графику функции, значит ее координаты удовлетворяют уравнению у=-х²-2х+6.
к=-(-3)²-2*(-3)+6 , к=-9+6+6 , к=3
Задание №2
Не вычисляя углов треугольника, определите его вид (по величине углов), если стороны треугольника равны.
а) 2,3 и 4
Тупоугольный, т.к. против большей стороны лежит больший угол.
б) 6,10 и 11
в) 8,15 и 17
Задание №3
Дан треугольник ABC
AB = 12 см
BC = 10 см
sin A = 0.2
sin C = ?
По теореме синусов
Отсюда
Задание №4
Рисунок приложил.
a) Решение. Из вершины С меньшего основания ВС трапеции АВСD опустим перпендикуляр СК на большее основание AD. Тогда СК = 8. Если AD = 21, ВС = 9 то
Если R - радиус окружности, описанной около трапеции ABCD , то
Объяснение:
у=х²+4х-2
Это парабола ,ветви вверх. Координаты вершины
а)х₀=-в/2а, х₀=(-4)/2=-2 , у₀=(-2)²+4*(-2)-2=-6 , (-2; -6).
б) во всех четвертях.
с) х=-2
d)Точки пересечения с осью ох, т.е у=0
х²+4х-2=0
Д=в²-4ас, Д=4²-4*4*(-2)=16+32=48=16*3
х₁=(-в+√Д):2а , х₁=(-4+4√3):2 , х₁=2(-2+2√3):2 , х₁=-2+2√3, (-2+2√3;0)
х₂=(-в-√Д):2а , х₂=(-4-4√3):2 , х₂=2(-2-2√3):2 , х₂=-2-2√3 , (-2-2√3;0)
Точки пересечения с осью оу, т.е. х=0, у=-2 (0;-2)
Доп.точки у=х²+4х-2 :
х: -5 -4 -3 1
у: 3 -2 -5 3
2)у=-х²-2х+6 Это парабола ,ветви вниз.
а)f(2)=-(2)²-2*2+6=-4-4+6=-2,
f(-2)=-(-2)²-2*(-2)+6=-4+4+6=6,
б) точка (-3;к) принадлежит графику функции, значит ее координаты удовлетворяют уравнению у=-х²-2х+6.
к=-(-3)²-2*(-3)+6 , к=-9+6+6 , к=3
Задание №2
Не вычисляя углов треугольника, определите его вид (по величине углов), если стороны треугольника равны.
а) 2,3 и 4
Тупоугольный, т.к. против большей стороны лежит больший угол.
б) 6,10 и 11
Тупоугольный, т.к. против большей стороны лежит больший угол.
в) 8,15 и 17
Тупоугольный, т.к. против большей стороны лежит больший угол.
Задание №3
Дан треугольник ABC
AB = 12 см
BC = 10 см
sin A = 0.2
sin C = ?
По теореме синусов
Отсюда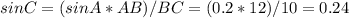
Задание №4
Рисунок приложил.
a) Решение. Из вершины С меньшего основания ВС трапеции АВСD опустим перпендикуляр СК на большее основание AD. Тогда СК = 8. Если AD = 21, ВС = 9 то
Если R - радиус окружности, описанной около трапеции ABCD , то