Тема: декартова система координат (с рисунком) :

1. среди данных точек к(-6,0,0), l(10,-5,0), м(0,6,0), n(7,-8,0), р(0,0,-20),q(0,11,-2) найдите те, которые принадлежат: а) оси оу; 6) оси oz; в) плоскости оху; г) плоскости оуz.

2. найдите координаты оснований перпендикуляров, опущенных из данных точек е(б,-2,8) и е(-3,2,-5) на: а) ось ох; 6) плоскость охz.

3. найдите координаты точек, симметричных точкам u(8,0,6), v(20,-14,0) относительно: а) плоскости оуz; 6) оси ох.

Дано: АВСД прямоугольник   Р=18 м, S= 20 м^2
Найти  АВ, ВС
Решение
пусть АВ=х   ВС=у
тогда периметр прямоугольника равен Р=2(х+у) =18
площадь равна S = x * y =20
получаем систему уравнений
2(х+у)=18
х*у=20
решаем ее
первое уравнение делим на 2 и выразим у
у=9-х подставим во второе уравнение
(9-х)х=20 раскроем скобки
9х - х^2 = 20 или x^2-9х +20 =0 решаем квадратное уравнение
дискриминант равен 1 корни х=4 и х=5
тогда соответственно у=9-х=9-4=5  и у=9-5=4
То есть стороны прямоугольника равны 4 и 5 или 5 и 4
ответ: 4; 5

1. Будем доказывать методом математической индукции.

Проверяем истинность утверждения при n = 1:

а) 2*49 + 16 + 40 = 154 = 11*14  -  делится на 11.

б) Предположим, что 2*7^(2k) + 16^k +8*5^k   - делится на 11. Где k - произвольное натуральное число.

в) Докажем, что тогда при n = k+1 полученное выражение - тоже делится на 11:

Теперь четко видно что оба больших слагаемых делятся на 11:

первое - исходя из предположения, второе - имеет 11 как общий сомножитель для своих слагаемых.

Итак мы доказали , что если при произвольном n= k выражение делится на 11, то и при n = k+1 выражение делится на 11.

Значит исходное выражение делится на 11.  что и требовалось доказать.

2)

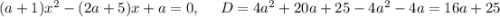
D>0    a>-25/16   a>-1,5625

Разбиваем ОДЗ на две части:

а) (-1; беск)

 

Первое из написанных неравенств верно. Проверим второе:

16a+25<16a^2+56a+49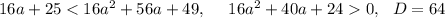

Корни  -1; -1,5   Решение с учетом ОДЗ: (-1; беск)

б) (-1,5625; -1)

 

Правая чать на выбранной области - отрицательна, что недопустимо. Здесь решений нет.

ответ: (-1; бескон).

3.

ответ: 1