а) x²-64<0 1. Переносим 64 и меняем знак, число становится положительным. x²<64 2. Избавляемся от степени. 64 это 8 во второй степени. x<8 Получаем диапазон меньше 8. Чертим график, выделяем часть до числа 8. Точка будет пустой, так как знак неравенства строгий. Получаем х∈(-∞,8). ответ: (-∞;8)
б) (х+2)(х+4)<0 1. Корни уравнения известны, -4 и -2 2. Решаем по методу интервала. Располагаем числа на графике, расставляем знаки поочередно (+ - +) Получаем отрицательное значение в промежутке от -4 до -2, это и будет нашим ответом, т.к. знак неравенства отрицательный. Точки будут пустыми, знак строгий. Получаем х∈(-4;-2). ответ: (-4;-2)
в) х²-6x-7≤0 1. Решаем квадратичное уравнение, находим корни. а=1; b= (-6); c= (-7) D= b²-4ac = (-6)²-4×1×(-7) = 36+28=64 x₁,₂= = x₁= = 7 x₂= = -1 2. Решаем по методу интервала. Располагаем числа на графике, расставляем знаки поочередно (+ - +) Получаем отрицательное значение в промежутке от -1 до 7, это и будет нашим ответом, т.к. знак неравенства отрицательный. Точки буду закрашенными, а скобки квадратными, т.к. знак неравенства нестрогий (≤). Получаем х∈[-1;7]. ответ: [-1;7]
1. а) значение аргумента равно 3, тогда значение функции:
б) Согласно условию значение функции равно 5, то есть,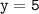
, то значение аргумента найдем, решив следующее уравнение:
в) Подставляя координаты точки В в график уравнения, получим
Раз выполняется тождество, следовательно, график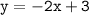
проходит через точку В(-1;5).
2. Графиком линейной функции является прямая. Для построения прямой достаточно взять две точки, например: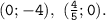
а) значению аргумента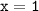
соответствует значение функции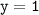 
б) значению функции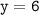
соответствует значение аргумента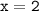 
3. Точки пересечения с осью координат Х. График функции пересекает ось Х при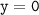
, значит нужно решить уравнение:
Точки пересечения с осью координат У. График пересекает ось У, когда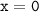
, то есть, подставляя х=0 в график уравнения, получим
4. Раз график функции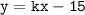
проходит через точку 
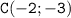, значит значение 
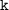найдем, подставив координаты точки C, имеем
1. Переносим 64 и меняем знак, число становится положительным.
x²<64
2. Избавляемся от степени. 64 это 8 во второй степени.
x<8
Получаем диапазон меньше 8. Чертим график, выделяем часть до числа 8. Точка будет пустой, так как знак неравенства строгий.
Получаем х∈(-∞,8).
ответ: (-∞;8)
б) (х+2)(х+4)<0
1. Корни уравнения известны, -4 и -2
2. Решаем по методу интервала.
Располагаем числа на графике, расставляем знаки поочередно (+ - +)
Получаем отрицательное значение в промежутке от -4 до -2, это и будет нашим ответом, т.к. знак неравенства отрицательный. Точки будут пустыми, знак строгий.
Получаем х∈(-4;-2).
ответ: (-4;-2)
в) х²-6x-7≤0
1. Решаем квадратичное уравнение, находим корни.
а=1; b= (-6); c= (-7)
D= b²-4ac = (-6)²-4×1×(-7) = 36+28=64
x₁,₂=
x₁=
x₂=
2. Решаем по методу интервала.
Располагаем числа на графике, расставляем знаки поочередно (+ - +)
Получаем отрицательное значение в промежутке от -1 до 7, это и будет нашим ответом, т.к. знак неравенства отрицательный. Точки буду закрашенными, а скобки квадратными, т.к. знак неравенства нестрогий (≤).
Получаем х∈[-1;7].
ответ: [-1;7]
Надеюсь