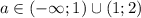// // [тема: производная] Задача: Тело движется по закону x(t) = t⁴ + 0,5t² – 3t; (x — в метрах, t — в секундах) Найдите скорость и ускорение тела через 2 с после начала движения.
Перенесём один из корней влево, а одну из семёрок — вправо следующим образом:
Рассмотрим функцию . Она представляет собой сумму двух монотонно возрастающих функций (показательная и функция корня седьмой степени), следовательно она также монотонно возрастает. Значит, каждому аргументу соответствует ровно одно значение функции, то есть функция f(x) взаимно однозначна.
Уравнение в таком случае принимает следующий вид:
Поскольку каждому значению функции соответствует только одно значение аргумента, равенство значений функции можно свести к равенству её аргументов:
Если , то это линейное уравнение, имеющее не более одного корня, что не подходит.
Если , то это квадратное уравнение. Оно имеет два корня при положительном дискриминанте:
1) 6+10+11=27(см)-P-ровностороннего триугольника 2) 27:3=9(см)-будет равна сторона ровностороннего триугольника ответ:9 сантиметров будет равна сторона ровностороннего триугольника теперь объясню как делать объяснение: в 1 действии необходимо найти периметр формула(P=a+b+c) во втором действии мы делим периметр в этой задаче он равен 27 (P=27) делим на 3( поскольку сторон у треугольника 3) будет 9 и так как триугольник ровносторонний любая сторона этого триугальника будет равна 9 сантиметров
Объяснение:
Перенесём один из корней влево, а одну из семёрок — вправо следующим образом:
Рассмотрим функцию![f(x)=7^x+\sqrt[7]{x}](/tpl/images/4771/4253/5e929.png) . Она представляет собой сумму двух монотонно возрастающих функций (показательная и функция корня седьмой степени), следовательно она также монотонно возрастает. Значит, каждому аргументу соответствует ровно одно значение функции, то есть функция f(x) взаимно однозначна.
. Она представляет собой сумму двух монотонно возрастающих функций (показательная и функция корня седьмой степени), следовательно она также монотонно возрастает. Значит, каждому аргументу соответствует ровно одно значение функции, то есть функция f(x) взаимно однозначна.
Уравнение в таком случае принимает следующий вид:
Поскольку каждому значению функции соответствует только одно значение аргумента, равенство значений функции можно свести к равенству её аргументов:
Если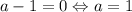 , то это линейное уравнение, имеющее не более одного корня, что не подходит.
, то это линейное уравнение, имеющее не более одного корня, что не подходит.
Если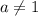 , то это квадратное уравнение. Оно имеет два корня при положительном дискриминанте:
, то это квадратное уравнение. Оно имеет два корня при положительном дискриминанте:
Учитывая, что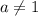 , получаем ответ
, получаем ответ