Тема степень и ее свойства 1. Как называется число 2 в выражении 5²?
выбор ответа:
индекс степени
показатель степени
основание степени

2. Найдите значение выражения -x² при x=3

3. Упростите выражение:
(y³*(y⁵)⁷:y¹):y²³
выбор ответа:
y
y⁴
y⁶
y⁵

4. Представьте в виде степени вырождение x⁵*x³
выбор ответа:
x⁸
x²
x¹²⁵
x¹⁵

5. Вычислите квадрат куба числа 3

6. Вычислите значение выражение : 6*2²+(-1)⁵

7. Вычислите значение частного степеней (2²*4³):2⁵

8. Как называется число 3 в выражение 3⁵?
выбор ответа:
индекс степени
основание степени
показатель степени

9. Какому числу куб числа -0,2?

10. Вычислите: -3³+0⁵+3²
​

Для графического решения заданное уравнение представим как равенство двух функций: 2^(x + 2) + 1 = -2х.

Точка пересечения их графиков даст корень.

Прямая у = -2х строится по двум точкам, например, х = 0, у = 0.

х = -3, у = 6.

Для построения функции у = (2^(x+2)) + 1 приводит таблицу точек.

x y

-4.0 1.25

-3.5 1.35

-3.0 1.5

-2.5 1.71

-2.0 2

-1.5 2.41

-1.0 3

-0.5 3.83

0 5

0.5 6.66

1.0 9

1.5 12.31

2.0 17.

Точка пересечения х = -1,30785.

Сумма двух последовательных целых чисел, между которыми находится корень уравнения, равна  (-2) + (-1) = -3.

1. (х+4)(х+6) 2. (х -3)(х - )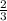

Объяснение:

1. х^2 +10x - 24

a=1, b=10, c=-24

Находим дискриминант и получаем D= 4

формулы x1 =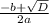 находим первый корень, который равен -4

А с формулы х2=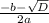 находим второй корень, который равен -6

Используем формулу квадратного трёхчлена ax^2+bx+c=a(x-x1)(x-x2)

Получаем:

x^2+10x-24= 1(x-(-4))(x-(-6)) = (x+4)(x+6)

2. 3x^2-11x+6

a=3, b=-11, c=6

Находим дискриминант и получаем D= 49

формулы x1 =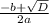 находим первый корень, который равен 3

А с формулы х2=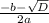 находим второй корень, который равен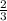

Используем формулу квадратного трёхчлена ax^2+bx+c=a(x-x1)(x-x2)

Получаем:

3x^2-11x+6= 1(x-3)(x-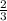 )