Область определения функции — это множество всех значений аргумента (переменной x). Другими словами, нам нужно найти при каких (х), функция возможна.
1. D(x)=(-∞;+∞) Какой бы мы (Х) не подставили, функция будет возможна.
2. D(x)=(-∞;+∞) Какой бы мы (Х) не подставили, функция будет возможна.
3.Когда есть дробь, должно выполнятся условие, что знаменатель ≠ 0
х-5≠0 х≠5
D(x)=(-∞;5)∪(5+∞);
4. Когда есть корень, есть правило, что под корнем стоит выражение, которое 0, откуда
х-50 х5
D(x)=[5;+∞)
5. Когда есть дробь, нельзя чтобы знаменатель был равен 0, и когда есть корень, есть правило, что под корнем стоит выражение, которое>0, откуда
4-х>0
-х>-4 домножим на (-1) и знаки поменяются
х<4
D(x)=(-∞;4)
6.Когда есть дробь, нельзя чтобы знаменатель был равен 0, откуда
-5≠0 ≠5
х₁≠√5
х₂≠-√5
D(x)=(-∞;-√5)∪(-√5;√5)∪(√5;+∞);
7. Когда есть дробь, нельзя чтобы знаменатель был равен 0, откуда
+4≠0 Выражение под квадратом всегда неотрицательное, значит х=R.
При любом значении (х), выражение +4≠0 не будет равно 0.
D(x)=(-∞;+∞)
8. Когда есть дробь, нельзя чтобы знаменатель был равен 0:
IxI-3≠0
IxI≠3
х₁≠3
х₂≠-3
D(x)=(-∞;-3)∪(-3;3)∪(3;+∞);
9. Когда есть дробь, нельзя чтобы знаменатель был равен 0:
IxI+5≠0
IxI≠-5, откуда x=R, тк любое выражение под модулем≥0
D(x)=(-∞;+∞) Другими словами, знаменатель при любом (х) не обернется в 0.
10. Когда есть корень, должно выполнятся условие, что выражение под нем ≥0. Когда есть дробь, должно выполнятся условие, что знаменатель ≠ 0. Составим систему:
Область определения функции — это множество всех значений аргумента (переменной x). Другими словами, нам нужно найти при каких (х), функция возможна.
1. D(x)=(-∞;+∞) Какой бы мы (Х) не подставили, функция будет возможна.
2. D(x)=(-∞;+∞) Какой бы мы (Х) не подставили, функция будет возможна.
3.Когда есть дробь, должно выполнятся условие, что знаменатель ≠ 0
х-5≠0 х≠5
D(x)=(-∞;5)∪(5+∞);
4. Когда есть корень, есть правило, что под корнем стоит выражение, которое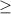
0, откуда
х-5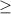
0 х
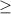5
D(x)=[5;+∞)
5. Когда есть дробь, нельзя чтобы знаменатель был равен 0, и когда есть корень, есть правило, что под корнем стоит выражение, которое>0, откуда
4-х>0
-х>-4 домножим на (-1) и знаки поменяются
х<4
D(x)=(-∞;4)
6.Когда есть дробь, нельзя чтобы знаменатель был равен 0, откуда
х₁≠√5
х₂≠-√5
D(x)=(-∞;-√5)∪(-√5;√5)∪(√5;+∞);
7. Когда есть дробь, нельзя чтобы знаменатель был равен 0, откуда
При любом значении (х), выражение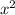
+4≠0 не будет равно 0.
D(x)=(-∞;+∞)
8. Когда есть дробь, нельзя чтобы знаменатель был равен 0:
IxI-3≠0
IxI≠3
х₁≠3
х₂≠-3
D(x)=(-∞;-3)∪(-3;3)∪(3;+∞);
9. Когда есть дробь, нельзя чтобы знаменатель был равен 0:
IxI+5≠0
IxI≠-5, откуда x=R, тк любое выражение под модулем≥0
D(x)=(-∞;+∞) Другими словами, знаменатель при любом (х) не обернется в 0.
10. Когда есть корень, должно выполнятся условие, что выражение под нем ≥0. Когда есть дробь, должно выполнятся условие, что знаменатель ≠ 0. Составим систему:
x-1≥0
x-10≠0
x≥1
x≠10
Запишем область определения:
D(x)=[1;10)(10+∞)
y=kx+b - уравнение прямой с угловым коэффициентом
Подставим в него координаты точек А и В
А (6;-4)
x=6; y=-4
-4=k·6+b
В (8;4)
x=8; y=4
4=k·8+b
Решаем систему двух уравнений и находим k и b:
y=2x-16 - уравнение прямой AB с угловым коэффициентом k=2
2x-y-16=0 - общее уравнение прямой АВ
б)
Параллельные прямые имеют одинаковые угловые коэффициенты
y=2x+b - уравнение прямых, параллельных АВ
Чтобы найти прямую, проходящую через точку С подставим координаты точки С
С (-1;6)
6=2·(-1)+b
b=8
y=2x+8 - уравнение прямой, параллельной АВ и проходящей через точку С.
2x-y+8=0 общее уравнение прямой, параллельной АВ и проходящей через точку С.
Произведение угловых коэффициентов взаимно перпендикулярных прямых равно (-1)
k₁·k₂=-1
k₁=2
k₂=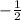
- угловой коэффициент прямой, перпендикулярной АВ
Подставляем координаты точки С:
x+2y-13=0- общее уравнение прямой, перпендикулярной АВ и проходящей через точку С
в)
Прямая, параллельная АВ и проходящей через точку С. пересекается с прямой, перпендикулярной АВ и проходящей через точку С в точке С.
Значит требуется найти точку пересечения прямой АВ и прямой, перпендикулярной АВ и проходящей через точку С
Решаем систему уравнений:
Приравниваем правые части уравнений:
х=9
y=2·9-16
y=2
О т в е т. (9;2)