Всё дело в том , что под знаком модуля может стоять и положительное число и отрицательное. |x| = x при х ≥ |x| = -x при х меньше 0 первый модуль = 0 при х = 3, второй =0 при х = -3 Вся числовая прямая этими точками разделится на промежутки: -∞ -3 3 +∞ На каждом промежутке функция будет выглядеть по - своему. а) (-∞; -3) у = -(х - 3) + х + 3 = -х +3 +х +3 = 6 у = 6 б) [-3;3] у = -(х -3) -(х +3) = -х +3 -х -3 = -2х у = -2х в) (3; +∞) у = х - 3-(х +3) = х - 3 - х - 3 = - 6 у = -6 теперь на координатной плоскости надо построить график этой кусочной функции. Теперь насчёт у = кх. Это прямая, проходящая через начало координат. Чтобы она имела с нашим графиком только одну точку пересечения, надо к выбирать любые, кроме к∈ (0; -2]
|x| = -x при х меньше 0
первый модуль = 0 при х = 3, второй =0 при х = -3
Вся числовая прямая этими точками разделится на промежутки:
-∞ -3 3 +∞
На каждом промежутке функция будет выглядеть по - своему.
а) (-∞; -3)
у = -(х - 3) + х + 3 = -х +3 +х +3 = 6
у = 6
б) [-3;3]
у = -(х -3) -(х +3) = -х +3 -х -3 = -2х
у = -2х
в) (3; +∞)
у = х - 3-(х +3) = х - 3 - х - 3 = - 6
у = -6
теперь на координатной плоскости надо построить график этой кусочной функции.
Теперь насчёт у = кх. Это прямая, проходящая через начало координат. Чтобы она имела с нашим графиком только одну точку пересечения, надо к выбирать любые, кроме к∈ (0; -2]
см. рисунок
Объяснение:
комбинация 1) у = х и 2)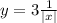 3) смещенная по у на -1.
3) смещенная по у на -1.
у = х вещь извесная
1/x тоже извесный график
1/|x| отразит часть 1/x, которая для отрицательніх иксов снизу вверх относительно Ох
минус 3 полностью перевернет єто все в минуса и растянет по оси 0у в три раза
если схрестить с х, то єто ве еще и перекосится приближая горизонтальные роги к у=х.
в значении х=0 будет разрыв плюс бесконечность
ну и -1 сместит это все по оси 0у на -1.
в результате будет чтото типа рисунка.
вручную строится по 7+ точкам например при х = -4, -3, -2, -1, -0,5; -0,25 +0,25;+0,5; 1; 2 ....