Данное уравнение равносильно уравнению
n ∈ Z
Рассмотрим более пристально выражение , которое можно записать в следующем виде:
Так как (сумма двух положительных взаимно обратных величин), , то , а значит,
Однако выражение должно быть целым, что возможно только при . Это равенство, в свою очередь, выполняется, если и только если
, k ∈ Z
ответ: , k ∈ Z
Данное уравнение равносильно уравнению
n ∈ Z
Рассмотрим более пристально выражение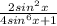 , которое можно записать в следующем виде:
, которое можно записать в следующем виде:
Так как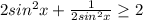 (сумма двух положительных взаимно обратных величин),
(сумма двух положительных взаимно обратных величин), 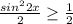 , то
, то 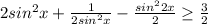 , а значит,
, а значит, 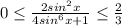
Однако выражение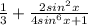 должно быть целым, что возможно только при
должно быть целым, что возможно только при 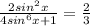 . Это равенство, в свою очередь, выполняется, если и только если
. Это равенство, в свою очередь, выполняется, если и только если
ответ: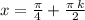 , k ∈ Z
, k ∈ Z