Войти
Регистрация
Спроси ai-bota
В
Все
М
Математика
О
ОБЖ
У
Українська мова
Х
Химия
Д
Другие предметы
Н
Немецкий язык
Б
Беларуская мова
М
Музыка
Э
Экономика
Ф
Физика
Б
Биология
О
Окружающий мир
У
Українська література
Р
Русский язык
Ф
Французский язык
П
Психология
О
Обществознание
А
Алгебра
М
МХК
Г
География
И
Информатика
П
Право
А
Английский язык
Г
Геометрия
Қ
Қазақ тiлi
Л
Литература
И
История
Показать больше
Показать меньше
sndzhychayana
04.07.2022 08:16 •
Алгебра
найти корни из компл.чисел
Показать ответ
Ответ:
RAYDEN02
09.10.2020 12:44
Рассмотрим комплексное число
, его модуль
. Тогда
Поскольку
то
0,0
(0 оценок)
Популярные вопросы: Алгебра
Lopsiwk
02.10.2020 15:40
Найди значение выражения 0,13⋅7000+(19) 2⋅27. ответ с дробью...
AngelGelay
26.09.2020 04:19
Решите уровнение 4x+2/7 + 3x-5/4=3 ...
БатонБагетович
23.08.2020 00:36
1. Решите неравенство: (х+2)∙(х-3) 0 A) (-2;3) B) (2;3) C) (-1;2) D) (-∞;-2)ᴗ(3;+∞) E) (-∞;2]ᴗ(3;+∞) 2. При каких значениях х значение квадратного трехчлена -х2-х+3...
danilarostov2
12.07.2022 04:22
Писок аденииУсловие задания:Реши систему уравнений методом подстановки...
еаае1ьп
17.08.2021 03:14
У и найдите значение алгебраической дроби, при m=5,n=10...
HardFunny
31.01.2020 18:14
Y = k / x (k ≠ 0), ее график и свойства Показано на рисунке и = используя часть гиперболы Икс ∈ [–5; –1] когда и = Найдите максимальное и минимальное значения функции....
10584869678
30.01.2020 22:30
Упростите выражение:12x-(2x-11) +(-3+9) ...
MrKreol
28.01.2021 16:31
Выполни следующие шесть уравнений...
карим113
16.09.2022 08:17
УПРОСТИТЬ ОДНОЧЛЕН(2cy^3)^2* 8c^5y/(4c^2*y)^3...
лоо25дллллл
31.08.2020 03:55
Представь выражения в виде произведения многочленов многочлены в скобках записывай в порядке убывания степеней (4m-7)^2-64= b^8-(b-4)^2=...
Полный доступ
Позволит учиться лучше и быстрее. Неограниченный доступ к базе и ответам от экспертов и ai-bota
Оформи подписку
О НАС
О нас
Блог
Карьера
Условия пользования
Авторское право
Политика конфиденциальности
Политика использования файлов cookie
Предпочтения cookie-файлов
СООБЩЕСТВО
Сообщество
Для школ
Родителям
Кодекс чести
Правила сообщества
Insights
Стань помощником
ПОМОЩЬ
Зарегистрируйся
Центр помощи
Центр безопасности
Договор о конфиденциальности полученной информации
App
Начни делиться знаниями
Вход
Регистрация
Что ты хочешь узнать?
Спроси ai-бота
Рассмотрим комплексное число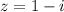 , его модуль
, его модуль 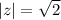 . Тогда
. Тогда
Поскольку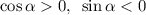 то
то