Пусть «» кг раствора было изначально ⇒ доля соли в этом растворе ⇒ кг раствора стало после добавления соли ⇒ доля соли в конечном растворе. Т.к. доля соли после добавления увеличилась на 15% (), получим:
Домножим обе части уравнения на и , получим:
Перенесём правую часть уравнения в левую, получим:
Квадратное уравнение вида можно решить с дискриминанта .
⇒ корней будет два.
По условию концентрация соли в первоначальном растворе была меньше 20% ⇒ (массовая доля соли в первоначальном растворе) должна быть .
Обозначим количество растений в одном ряду: х шт.
Тогда количество рядов: х + 8
Очевидно, что всего растений было высажено: х(х + 8) шт.
Так как по 3 растения в каждом ряду не прижились, то растений в ряду осталось: х - 3 шт.
Тогда: (х - 3)(х + 8) = 80
x² + 5x - 104 = 0 D = b²-4ac = 25+416 = 441 = 21²
x₁₂ = (-b±√D)/2a
x₁ = -13 - не удовлетворяет условию
х₂ = 8 - растений было посажено в каждом ряду.
Рядов всего: х + 8 = 16
Растений всего было высажено: 8 · 16 = 128 (шт.)
Погибло растений: 3 · 16 = 48 (шт.)
Потери рассады составили: 48 · 100 : 128 = 37,5%
30 кг
Объяснение:
Пусть « » кг раствора было изначально ⇒
» кг раствора было изначально ⇒ 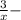 доля соли в этом растворе ⇒
доля соли в этом растворе ⇒ 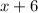 кг раствора стало после добавления соли ⇒
кг раствора стало после добавления соли ⇒ 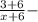 доля соли в конечном растворе. Т.к. доля соли после добавления увеличилась на 15% (
доля соли в конечном растворе. Т.к. доля соли после добавления увеличилась на 15% (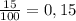 ), получим:
), получим:
Домножим обе части уравнения на и
и 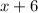 , получим:
, получим:
Перенесём правую часть уравнения в левую, получим:
Квадратное уравнение вида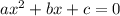 можно решить с дискриминанта
можно решить с дискриминанта 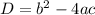 .
.
По условию концентрация соли в первоначальном растворе была меньше 20% ⇒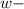 (массовая доля соли в первоначальном растворе) должна быть
(массовая доля соли в первоначальном растворе) должна быть 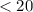 .
.
Значит, первоначальная масса раствора была 30 кг.