Объяснение: Ищем ОДЗ. Одновременно должны выполняться три условия :
Решением первого неравенства является объединение полуинтервалов (-∞; -1] ∪ [8; +∞) (вложение), решение второго - [-1; +∞), решение третьего - (-∞; 8]. Условия выполняются одновременно, поэтому нужно искать пересечение этих промежутков - им является множество {-1; 8}.
Так как ОДЗ удовлетворяют только два числа, можем спокойно их подставить в наше неравенство и посмотреть, какие из них являются решением.
При х = -1 получаем: - верное неравенство. х = -1 - решение.
При х = 8 получаем: - неверное неравенство. Следовательно, х = 8 не является решением.
Объяснение: Ищем ОДЗ. Одновременно должны выполняться три условия :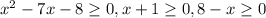
Решением первого неравенства является объединение полуинтервалов (-∞; -1] ∪ [8; +∞) (вложение), решение второго - [-1; +∞), решение третьего - (-∞; 8]. Условия выполняются одновременно, поэтому нужно искать пересечение этих промежутков - им является множество {-1; 8}.
Так как ОДЗ удовлетворяют только два числа, можем спокойно их подставить в наше неравенство и посмотреть, какие из них являются решением.
При х = -1 получаем: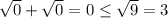 - верное неравенство. х = -1 - решение.
- верное неравенство. х = -1 - решение.
При х = 8 получаем: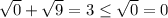 - неверное неравенство. Следовательно, х = 8 не является решением.
- неверное неравенство. Следовательно, х = 8 не является решением.
Все случаи перебрали. Запишем ответ.
ОТВЕТ: -1.