Легко побачити, що кожне число збільшується на 5 тому задаємо арифметичну прогресію з першим членом – 1 і різницею – 5:
Оскільки ми не знаємо порядковий номер х-а, запишемо йому номер n:
У рівнянні маємо суму чисел послідовності.
Загальна формула суми арифметичної прогресії:
Підставимо у формулу відомі нам складові:
За умовою дана сума дорівнює 342, тоді:
Оскільки n – порядковий номер члена прогресії, він не може бути від'ємний тому n ≠ -57/5 => n = 12.
Так як ми знаємо n, ми можемо знайти x:
Відповідь: 56
Первый
Решение ищем как сумму общего решения однородного уравнения, соответствующего данному неоднородному, и частного решения данного неоднородного уравнения.
Составим однородное уравнение, соответствующее данному неоднородному:
Решаем уравнение с разделяющимися переменными:
Общее решение однородного уравнения:
Частное решение ищем в виде .
Найдем производную:
Подставим в уравнение:
Условие равенства левой и правой частей:
Частное решение неоднородного уравнения:
Искомое решение:
Второй
Решение ищем в виде произведения двух ненулевых функций . Тогда .
Пусть сумма первого и третьего слагаемого в левой части равна нулю:
Тогда второе слагаемое в левой части равно правой части:
Интеграл вычислим отдельно. Будем использовать интегрирование по частям: (не записывая произвольную константу):
Таким образом:
Искомая функция:
Легко побачити, що кожне число збільшується на 5 тому задаємо арифметичну прогресію з першим членом – 1 і різницею – 5:
Оскільки ми не знаємо порядковий номер х-а, запишемо йому номер n:
У рівнянні маємо суму чисел послідовності.
Загальна формула суми арифметичної прогресії:
Підставимо у формулу відомі нам складові:
За умовою дана сума дорівнює 342, тоді:
Оскільки n – порядковий номер члена прогресії, він не може бути від'ємний тому n ≠ -57/5 => n = 12.
Так як ми знаємо n, ми можемо знайти x:
Відповідь: 56
Первый
Решение ищем как сумму общего решения однородного уравнения, соответствующего данному неоднородному, и частного решения данного неоднородного уравнения.
Составим однородное уравнение, соответствующее данному неоднородному:
Решаем уравнение с разделяющимися переменными:
Общее решение однородного уравнения:
Частное решение ищем в виде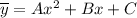 .
.
Найдем производную:
Подставим в уравнение:
Условие равенства левой и правой частей:
Частное решение неоднородного уравнения:
Искомое решение:
Второй
Решение ищем в виде произведения двух ненулевых функций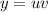 . Тогда
. Тогда 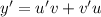 .
.
Пусть сумма первого и третьего слагаемого в левой части равна нулю:
Тогда второе слагаемое в левой части равно правой части:
Интеграл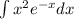 вычислим отдельно. Будем использовать интегрирование по частям:
вычислим отдельно. Будем использовать интегрирование по частям: 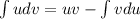 (не записывая произвольную константу):
(не записывая произвольную константу):
Таким образом:
Искомая функция: