Алгебра: tgx -1/2 sin(x+π/4) √3/2

tgx -1/2
sin(x+π/4)> √3/2

Показать ответ

Ответ:

катяlove4

15.05.2022 22:24

Биквадратное уравнение.

Решается заменой переменной:

x^2=t

t^2+(3a+1)t+0,25=0

$D=(3a+1)^2-4\cdot 0,25=9a^2+6a+1-1=9a^2+6a$

Если D >0, т.е.

$9a^2+6a0\\\\3a(3a+2) 0$

$a\in (-\infty; -\frac{2}{3})U(0;+\infty)$

уравнение имеет корни:

$t_{1}=\frac{-(3a+1)-\sqrt{9a^2+6a} }{2}$ или $t_{2}=\frac{-(3a+1)+\sqrt{9a^2+6a} }{2}$

Обратный переход:

$x^2=\frac{-(3a+1)-\sqrt{9a^2+6a} }{2}$ или $x^2=\frac{-(3a+1)+\sqrt{9a^2+6a} }{2}$

Уравнение x^2=с имеет корни, если c> 0, тогда корни противоположны по знаку

Чтобы корни данного уравнения были равны,

с=0

$\frac{-(3a+1)-\sqrt{9a^2+6a} }{2}=0$

$\sqrt{ 9a^2+6a}=-(3a+1)$

Это иррациональное уравнение.

При (3a+1) >0 оно не имеет корней.

При (3а+1) ≤0

возводим обе части уравнения в квадрат:

9a^2+6a=9a^2+6a+1

0=1 - неверно, нет таких значений а

Аналогично

$\frac{-(3a+1)+\sqrt{9a^2+6a} }{2}=0$

$\sqrt{ 9a^2+6a}=(3a+1)$

При (3a+1) < 0 оно не имеет корней.

При (3а+1) ≥0

возводим обе части уравнения в квадрат:

9a^2+6a=9a^2+6a+1

0=1 - неверно, нет таких значений а

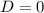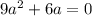
Если D=0 , т.е 9a^2+6a=0

a=0 или $a=-\frac{2}{3}$

При a=0

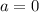
уравнение принимает вид:

x^4+x^2+0,25=0

$D=1^2-4\cdot 0,25=0$ ⇒ x^2=-1

уравнение не имеет корней

При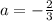 $a=-\frac{2}{3}$

уравнение принимает вид:

x^4-x^2+0,25=0

$D=1-4\cdot 0,25=0$ ⇒ $x^2=\frac{1}{2}$

$x=\pm\frac{\sqrt{2} }{2}$

Уравнение 4-ой степени, значит

$x_{1,2}=-\frac{\sqrt{2} }{2}$ и $x_{3,4}=\frac{\sqrt{2} }{2}$

О т в е т. При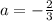 $a=-\frac{2}{3}$

0,0(0 оценок)

Ответ:

Vikanigmatulina

25.02.2021 11:29

∃ - квантор существования, читается "существует"

∀ - квантор всеобщности, читается "для любого"

Рассмотрим высказывания:

∃x ∃y x+y=2

"существует х и существует у, такие что выполняется условие х+у=2"

Истина. Действительно, такие числа существуют, например (1; 1), (2.5; -0.5) и т.д.

∀x ∀y x+y=2

"для любого х и для любого у выполняется условие х+у=2"

Ложь. Очевидно, не любые два числа в сумме дают 2. Например, это условие не выполняется для чисел (0; 1), (2; -0.5) и т.д.

∃x ∀y x+y=2

"существует х, такой что для любого у выполняется условие х+у=2"

Ложь. Предположим, что существует такой х, равный х₀. Тогда, выразив из формулы у, получим: у=2-х₀. Но так как х₀ - некоторая найденная константа, то и выражение (2-х₀) представляет собой константу. Но левая часть соответствует у, который может быть любым. Константа не может равняться одновременно любому выражению. Значит, такого х существовать не может. Например, если х=3, то равенство выполняется только при условии у=2-3=-1, пара (3; -1), ни при каком другом у с тем же х условие не выполняется.

∀x ∃y x+y=2

"для любого х, существует у, такой что выполняется условие х+у=2"

Истина. Выбирая "любой" х мы всегда можем вычислить соответствующее значение у по формуле у=2-х. Например, если х=π, то у=2-π, пара (π; 2-π), если х=0, то у=2-0=2, пара (0; 2), и т.д.

ответ: истинные высказывания 1, 4; ложные высказывания 2, 3

0,0(0 оценок)

Популярные вопросы: Алгебра