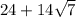x₁ = 1 ; x₂ = 5,5
Объяснение:
(2x+3)/(x^2-4x+4) - (x-1)/(x^2-2x) = 5/x ; ОДЗ: x^2-4x+4≠0 => (x-2)^2≠0 => x≠2 ; x^2-2x≠0 ; x(x-2)≠0 => x≠0
x ≠ 2 ; x ≠ 0
(2x+3)/((x-2)^2) - (x-1)/(x(x-2)) - 5/x = 0
(x(2x+3)-(x-2)(x-1)-5(x-2)^2)/(x(x-2)^2) = 0
(2x^2+3x-(x^2-x-2x+2)-5(x^2-4x+4))/(x(x^2-4x+4)) = 0 | · x(x^2-4x+4)
2x^2+3x-(x^2-x-2x+2)-5(x^2-4x+4) = 0
2x^2+3x-x^2+3x-2-5x^2+20x-20 = 0
x^2+6x-2-5x^2+20x-20 = 0
-4x^2 + 26x - 22 = 0 | : (-2)
2x^2 - 13x + 11 = 0
D = (-13)^2 - 4 · 2 · 11 = 169 - 88 = 81
x₁ = (13 - 9) / 4 = 4 / 4 = 1
x₂ = (13 + 9) / 4 = 22 / 4 = 11 / 2 = 5,5
x₁ = 1, x₂ = 5,5 ; x ≠ 2, x ≠ 0
А8.
ОДЗ:
Так как , то
_____________-7////////////////////////////////2________________________
-6; -5; -4; -3; -2; -1; 0; 1 - целые из этого промежутка
Исключаем по ОДЗ и находим сумму:
ответ: 19
А9.
Пусть - длина основания;
- ширина основания;
- высота параллелепипеда, тогда по т. Пифагора выразим диагонали каждой грани через стороны:
1) Сложим эти уравнения:
2)
=>
3)
4)
5)
ответ:
x₁ = 1 ; x₂ = 5,5
Объяснение:
(2x+3)/(x^2-4x+4) - (x-1)/(x^2-2x) = 5/x ; ОДЗ: x^2-4x+4≠0 => (x-2)^2≠0 => x≠2 ; x^2-2x≠0 ; x(x-2)≠0 => x≠0
x ≠ 2 ; x ≠ 0
(2x+3)/((x-2)^2) - (x-1)/(x(x-2)) - 5/x = 0
(x(2x+3)-(x-2)(x-1)-5(x-2)^2)/(x(x-2)^2) = 0
(2x^2+3x-(x^2-x-2x+2)-5(x^2-4x+4))/(x(x^2-4x+4)) = 0 | · x(x^2-4x+4)
2x^2+3x-(x^2-x-2x+2)-5(x^2-4x+4) = 0
2x^2+3x-x^2+3x-2-5x^2+20x-20 = 0
x^2+6x-2-5x^2+20x-20 = 0
-4x^2 + 26x - 22 = 0 | : (-2)
2x^2 - 13x + 11 = 0
D = (-13)^2 - 4 · 2 · 11 = 169 - 88 = 81
x₁ = (13 - 9) / 4 = 4 / 4 = 1
x₂ = (13 + 9) / 4 = 22 / 4 = 11 / 2 = 5,5
x₁ = 1, x₂ = 5,5 ; x ≠ 2, x ≠ 0
А8.
Так как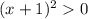 , то
, то
_____________-7////////////////////////////////2________________________
-6; -5; -4; -3; -2; -1; 0; 1 - целые из этого промежутка
Исключаем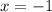 по ОДЗ и находим сумму:
по ОДЗ и находим сумму:
ответ: 19
А9.
Пусть - длина основания;
- длина основания;
1) Сложим эти уравнения:
2)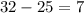
3)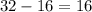
4)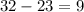
5)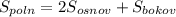
ответ: