1). Находим производную: y'= 5 x^4 +60 x^2 - 65 2). Приравниваем к нулю: 5 x^4 +60 x^2 - 65=0 , делим на 5 обе части и получаем
x^4 +12 x^2 - 13=0
Представляем x^4 как (x^2) ^2 и делаем замену x^2=t, тогда получаем: t^2+12t-13=0 Решаем квадратное уравнение:
D=196 t=1 и t=-13, где второе нам не подходит, т.к. отрицательное число. Возвращаемся к замене x^2=1 x=1 и x=-1, где x=1 не подходит, т.к. не входит в промежуток.
3). Находим значение на концах промежутка и на получившемся корне: y(-4)= -2044 y(0)=0 y(-1)=44 4). ответ: 44
1. Найти точку минимума функции: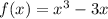
Найдём производную: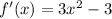
Приравняем производную к нулю:
Рисуем координатную ось и проверяем знаки, получаем: + - +
Точка минимума: с - на +
ответ: 1
2. Найдите наименьшее значение функции на отрезке [0;3]
Из ранее вычисленного проверяем точки, которые подходят в заданный отрезок [0;3]. Из этого следует, что точка -1 не подходит.
Считаем в точке.
f(0)= 0
f(3)=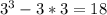
f(1)=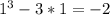
ответ: -2
3. Найдите значение функции в точке максимума: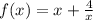
Одна точка и она же максимум.
ответ: 1,25
1). Находим производную: y'= 5 x^4 +60 x^2 - 65
2). Приравниваем к нулю: 5 x^4 +60 x^2 - 65=0 , делим на 5 обе части и получаем
x^4 +12 x^2 - 13=0
Представляем x^4 как (x^2) ^2 и делаем замену x^2=t, тогда получаем:
t^2+12t-13=0
Решаем квадратное уравнение:
D=196
t=1 и t=-13, где второе нам не подходит, т.к. отрицательное число.
Возвращаемся к замене x^2=1 x=1 и x=-1, где x=1 не подходит, т.к. не входит в промежуток.
3). Находим значение на концах промежутка и на получившемся корне:
y(-4)= -2044
y(0)=0
y(-1)=44
4). ответ: 44