Только один пример. Интересует решение, а не только ответ. Найдите значения аргумента, удовлетворяющие условию f'(x)(знак меньше/равно)g'(x), если f(x)=xcosx, g(x)=sinx
У = 2 + 3·|cosх| Известно, что косинус может принимать значения от - 1 до 1. -1 ≤ cosx ≤ 1 Если косинус стоит под знаком модуля, то 0 ≤ |cosх| ≤1. Умножим все части неравенства на 3: 0 ≤ 3|cosх| ≤ 3 Прибавим 2: 0 + 2 ≤ 2 + 3|cosх| ≤ 3 + 2 2 ≤ 2 + 3|cosх| ≤ 5 2 ≤ у ≤ 5 ответ: множество значений функции у ∈ [2; 5] Можно рассуждать немного иначе: Наименьшее значение, которое может принимать |cosх| - это 0. Тогда наименьшее значение функции у(0) = 2 + 3·0 = 2 Наибольшее значение, которое может принимать |cosх| - это 1. Тогда наибольшее значение функции у(1) = 2 + 3·1 = 5 Функция принимает значения от 2 до 5. множество значений функции у ∈ [2; 5]
№1.
Объяснение:
Пусть сторона 1-го квадрата равна А, а сторона 2-го равна В. Тогда можно составить систему уравнений:
Выражаем значение одной из переменных из 1-го уравнения и подставляем во 2-е:
Домножим все слагаемые на B^2, и затем заменим B^2 на t:
Значение t1 меньше 0, что не соответствует здравому смыслу, поэтому его не рассматриваем.
ответ: 3 и 4 см
-----------------
№2.
Объяснение:
Пусть один катет равен a, второй равен b. Тогда, исходя из теоремы Пифагора, составим систему уравнений:
Выразим одну из переменных из 2-го уравнения и подставим в 1-е:
Таким образом, катеты равны 5 и 12 см. Площадь такого треугольника будет равна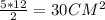
ответ: 30 см^2
Известно, что косинус может принимать значения от - 1 до 1.
-1 ≤ cosx ≤ 1
Если косинус стоит под знаком модуля, то 0 ≤ |cosх| ≤1.
Умножим все части неравенства на 3:
0 ≤ 3|cosх| ≤ 3
Прибавим 2:
0 + 2 ≤ 2 + 3|cosх| ≤ 3 + 2
2 ≤ 2 + 3|cosх| ≤ 5
2 ≤ у ≤ 5
ответ: множество значений функции у ∈ [2; 5]
Можно рассуждать немного иначе:
Наименьшее значение, которое может принимать |cosх| - это 0. Тогда наименьшее значение функции у(0) = 2 + 3·0 = 2
Наибольшее значение, которое может принимать |cosх| - это 1. Тогда наибольшее значение функции у(1) = 2 + 3·1 = 5
Функция принимает значения от 2 до 5.
множество значений функции у ∈ [2; 5]