а) При сравнении десятичных дробей в первую очередь нужно сравнивать целые части (они расположены слева от запятой). Так как целые части равны, то сравниваем дробные части
0.382 < 3*2 ⇔ 0.382 < 0.392 ⇒ потому что
Следовательно, 5.382 < 5.392
б) Аналогично, целые части равны, тогда сравниваем дробные части
0.* < 0.2 ⇔ 0.1 < 0.2 так как
Следовательно, 31.1 < 31.2
в) У первого числа символов после запятой не совпадает со вторым числом, тогда к дроби наименьшим количеством символов приписываем нули и сравним получившиеся числа дробных частей
3) Первый предел равен нулю, т.к. знаменатель быстрее стремится к бесконечности. И есть правило, если х стремится к бесконечности, то смотрим на стандартный вид многочленов числителя и знаменателя, если степень многочлена, стоящего в числителе выше, чем степень многочлена знаменателя, то ответ бесконечность, если ниже, то нуль, у нас как раз этот случай, а если показатели степеней равны, то ищем при максимальных одинаковых показателях отношение коэффициентов.
6) Во втором пределе если подставить 3, числитель обратится в нуль, ровно как и знаменатель, эту неопределенность устраняют разложением числителя на множители (х-3)(х²+3х+9²)/(х-3) и сокращением на (х-3), тогда после сокращения получим 3²+3*3+9=27
9) У третьего предела такая же беда. Разложим по формуле числитель и вынесем за скобку общий множитель из знаменателя, убираем неопределенность путем сокращения дроби.
а) При сравнении десятичных дробей в первую очередь нужно сравнивать целые части (они расположены слева от запятой). Так как целые части равны, то сравниваем дробные части
0.382 < 3*2 ⇔ 0.382 < 0.392 ⇒ потому что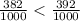
Следовательно, 5.382 < 5.392
б) Аналогично, целые части равны, тогда сравниваем дробные части
0.* < 0.2 ⇔ 0.1 < 0.2 так как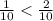
Следовательно, 31.1 < 31.2
в) У первого числа символов после запятой не совпадает со вторым числом, тогда к дроби наименьшим количеством символов приписываем нули и сравним получившиеся числа дробных частей
0.10 > 0.*1 ⇔ 0.10 > 0.01 так как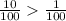
Следовательно, 7.1 > 7.01
г) Аналогично с примера в), рассуждения такие же:
0.010 < 0.*08 ⇔ 0.010 < 0.108 потому что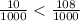
Следовательно, 7.01 < 7.108
3) Первый предел равен нулю, т.к. знаменатель быстрее стремится к бесконечности. И есть правило, если х стремится к бесконечности, то смотрим на стандартный вид многочленов числителя и знаменателя, если степень многочлена, стоящего в числителе выше, чем степень многочлена знаменателя, то ответ бесконечность, если ниже, то нуль, у нас как раз этот случай, а если показатели степеней равны, то ищем при максимальных одинаковых показателях отношение коэффициентов.
6) Во втором пределе если подставить 3, числитель обратится в нуль, ровно как и знаменатель, эту неопределенность устраняют разложением числителя на множители (х-3)(х²+3х+9²)/(х-3) и сокращением на (х-3), тогда после сокращения получим 3²+3*3+9=27
9) У третьего предела такая же беда. Разложим по формуле числитель и вынесем за скобку общий множитель из знаменателя, убираем неопределенность путем сокращения дроби.
(х-1)²/(х*(х-1)(х+1))=(х-1)/(х*(х+1))=(1-1)/(1*2)=0
ответ 3) 0
6)27
9) 0