Проверка: так как события А2...А12 несовместны и притом образуют полную группу, то p(A2)+p(A3)+...+p(A12)=1. Действительно, 1/36+2/36+3/36+4/36+5/36+6/36+5/36+4/36+3/36+2/36+1/36=36/36=1 - значит, вероятности найдены верно.
2) Число m1, которыми можно получить 3 орла при 5 бросаниях монеты, определяется по формуле m1=C(5,3)=10, где C(n,k) - число сочетаний из n по k. А так как вероятность любого p=1/2*1/2*1/2*1/2*1/2=1/32, то вероятность появления 3 орлов при 5 бросаниях монеты p1=10*p=10/32. Число m2, которыми можно получить 5 орлов при 7 бросаниях монеты, определяется по формуле m2=C(7,5)=21. А так как вероятность любого p2=1/2*1/2*1/2*1/2*1/2*1/2*1/2=1/128, то вероятность появления 5 орлов при 7 бросаниях монеты p2=21*p=21/128. Так как p1>p2, то первое событие более вероятно.
ответ: 1) M[X]=7; 2) более вероятно выпадение 3 орлов при 5 бросаниях монеты.
Объяснение:
1) Случайная величина X - число очков при бросаниях двух кубиков - может принимать значения от 2 до 12.
Событие А2 - выпало 2 очка - может реализоваться только одним :
- на 1 кубике выпало 1 очко и на 2 - тоже 1 очко.
Событие А3 - выпало 3 очка - может реализоваться следующими двумя :
1 и 2 или 2 и 1
Событие А4 - выпало 4 очка:
1 и 3 или 2 и 2 или 3 и 1 - всего .
Событие А5 - выпало 5 очков:
1 и 4 или 2 и 3 или 3 и 2 или 3 и 1 - всего .
Событие А6 - выпало 6 очков:
1 и 5 или 2 и 4 или 3 и 3 или 4 и 2 или 5 и 1 - всего .
Событие А7 - выпало 7 очков:
1 и 6 или 2 и 5 или 3 и 4 или 4 и 3 или 5 и 2 или 6 и 1 - всего .
Событие А8 - выпало 8 очков:
2 и 6 или 3 и 5 или 4 и 4 или 5 и 3 или 6 и 2 - всего .
Событие А9 - выпало 9 очков:
3 и 6 или 4 и 5 или 5 и 4 или 6 и 3 - всего .
Событие А10 - выпало 10 очков:
4 и 6 или 5 и 5 или 6 и 4 - всего .
Событие А11 - выпало 11 очков:
5 и 6 или 6 и 5 - всего .
Событие А12 - выпало 12 очков:
6 и .
Найдём вероятности этих событий. Так как вероятности всех одинаковы и равны 1/6*1/6=1/36, а сами являются несовместными событиями, то:
p(A2)=p(A12)=1*1/36=1/36; p(A3)=p(A11)=2*1/36=2/36; p(A4)=p(A10)=3*1/36=3/36; p(A5)=p(A9)=4*1/36=4/36; p(A6)=p(A8)=5*1/36=5/36; p(A7)=6*1/36=6/36.
Проверка: так как события А2...А12 несовместны и притом образуют полную группу, то p(A2)+p(A3)+...+p(A12)=1. Действительно, 1/36+2/36+3/36+4/36+5/36+6/36+5/36+4/36+3/36+2/36+1/36=36/36=1 - значит, вероятности найдены верно.
Составляем таблицу распределения случайной величины X:
xi 2 3 4 5 6 7 8 9 10 11 12
pi 1/36 2/36 3/36 4/36 5/36 6/36 5/36 4/36 3/36 2/36 1/36
Математическое ожидание M[X}=∑xi*pi=252/36=7.
2) Число m1, которыми можно получить 3 орла при 5 бросаниях монеты, определяется по формуле m1=C(5,3)=10, где C(n,k) - число сочетаний из n по k. А так как вероятность любого p=1/2*1/2*1/2*1/2*1/2=1/32, то вероятность появления 3 орлов при 5 бросаниях монеты p1=10*p=10/32. Число m2, которыми можно получить 5 орлов при 7 бросаниях монеты, определяется по формуле m2=C(7,5)=21. А так как вероятность любого p2=1/2*1/2*1/2*1/2*1/2*1/2*1/2=1/128, то вероятность появления 5 орлов при 7 бросаниях монеты p2=21*p=21/128. Так как p1>p2, то первое событие более вероятно.
Стороны клумбы: a = 5, b = 8
Объяснение:
Периметр прямоугольника P = 2(a+b) = 26
или a+b=13
Примем площадь меньшего пристроенного участка за S, его сторона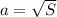
Площадь большего пристроенного участка равна S+39, его сторона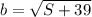
теперь решим ур-е:
Площадь большего пристроенного квадратного уч-ка равна S+39=64. Его сторона b = 8.
Прямоугольная клумба имеет размеры 5х8. Проверим периметр:
2*(5+8)=26
26=26, что и требовалось решить