Первое уравнение log3 (2-x)-1=log3 5 +log3(x+4) Для начала ,чтобы не попасть впросак определим область определения уравнения О.О.У. 2-х>0 х+4>0 Всё это объедини системой Получим х<2 х>-4 тоже знак системы поставь выбираем утверждение из этих двух которое будет включать одновременно и первое и второе х€(-4;2)-это О.О.У. Теперь приступим решать само уравнение прологарифмируем сразу -1 по основанию 3 получим уравнение в таком виде log3 (2x-1)-log3 1/3=log3 5 + log3(x+4) Вооот!! теперь всё прекрасно осталось два шага всего воспользуемся свойствами тогда получим в первом перейдём от разности к делению а во втором от сложения к умножению(не удивляйтесь это всё свойства мать их) log3 (2х-1) : 1/3))=log3 (5x+20) log3(6x-3)=log3(5x+20) Теперь потенцируем то бишь избавляемся от логарифмов 6х-3=5х+20 х=23-енто не входит в О.О.У. значит решений нет-с!
log3 (2-x)-1=log3 5 +log3(x+4)
Для начала ,чтобы не попасть впросак определим область определения уравнения
О.О.У.
2-х>0
х+4>0
Всё это объедини системой
Получим
х<2
х>-4
тоже знак системы поставь
выбираем утверждение из этих двух которое будет включать одновременно и первое и второе
х€(-4;2)-это О.О.У.
Теперь приступим решать само уравнение
прологарифмируем сразу -1 по основанию 3 получим уравнение в таком виде
log3 (2x-1)-log3 1/3=log3 5 + log3(x+4)
Вооот!! теперь всё прекрасно осталось два шага всего
воспользуемся свойствами тогда получим в первом перейдём от разности к делению а во втором от сложения к умножению(не удивляйтесь это всё свойства мать их)
log3 (2х-1) : 1/3))=log3 (5x+20)
log3(6x-3)=log3(5x+20)
Теперь потенцируем то бишь избавляемся от логарифмов
6х-3=5х+20
х=23-енто не входит в О.О.У.
значит решений нет-с!
Могу предложить несколько корявое, но все же решение... наверное.
Обозначим за a и b цифры искомого числа. Тогда из условия задачи это число есть
приравняем выражения, будем считать a переменной величиной, а b какой-то постоянной, тогда это будет квадратным уравнением относительно a :
Решая обычным образом находим
Мы знаем, что a и b - цифры, т.е. они могут быть лишь величинами 0 1 2 3 4 5 6 7 8 9
Смотрим, при самых очевидных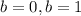
корень нормально извлекается.
Тогда
Из всех возможных двузначных чисел (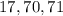
) подходящим оказывается только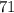 
Подтвердить это можно только непосредственной проверкой