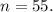В знаменателе минусы уничтожаются (минус на минус дает плюс). 3x^2 - x + 3 ≠ 0 D = (-1)^2 - 4*3*3 = 1 - 36 < 0 - корней нет. 3x^2 - x + 3 > 0 при любом x. (x - 2)^2 > 0 при любом x, кроме x = 2, где (x - 2)^2 = 0 Поэтому x = 2 - это решение. Делим на всё это, а также сокращаем (x - 1). Но нужно помнить, что x = 2 - решение, а x = 1 - не решение. Особые точки: x = -7 и x = 2/3 По методу интервалов берем любое число, например, 0 Неравенство выполнено, значит, интервал (-7; 2/3] подходит. Точка x = 1 в интервал не входит. ответ: x ∈ (-7; 2/3] U [2]
3) Это арифметическая прогрессия с разностью –5. Продолжается так: 6,7; 6,2; 5,7; 5,2; 4,7; 4,2; 3,7; 3,2 ...
4) Первое число кратное трём, это тройка. Поэтому подходят либо второй, либо третий вариант. Четвёртый член должен быть равен 3*4=12, поэтоу правильный ответ — второй: 3; 12; 33.
5)
6)
7) Это арифметическая прогрессия.
8)
ответ: нет, не является, потому что должно быть натуральным числом.
9)
Наибольшее натуральное , удовлетворяющее этому неравенству, — это 16.
ответ: 16 членов.
10)
Второе решение не подходит, поскольку должно быть натуральным числом.
В знаменателе минусы уничтожаются (минус на минус дает плюс).
3x^2 - x + 3 ≠ 0
D = (-1)^2 - 4*3*3 = 1 - 36 < 0 - корней нет.
3x^2 - x + 3 > 0 при любом x.
(x - 2)^2 > 0 при любом x, кроме x = 2, где (x - 2)^2 = 0
Поэтому x = 2 - это решение.
Делим на всё это, а также сокращаем (x - 1).
Но нужно помнить, что x = 2 - решение, а x = 1 - не решение.
Особые точки: x = -7 и x = 2/3
По методу интервалов берем любое число, например, 0
Неравенство выполнено, значит, интервал (-7; 2/3] подходит.
Точка x = 1 в интервал не входит.
ответ: x ∈ (-7; 2/3] U [2]
1) Аналитический.
2) Рекуррентній.
3) Это арифметическая прогрессия с разностью –5. Продолжается так: 6,7; 6,2; 5,7; 5,2; 4,7; 4,2; 3,7; 3,2 ...
4) Первое число кратное трём, это тройка. Поэтому подходят либо второй, либо третий вариант. Четвёртый член должен быть равен 3*4=12, поэтоу правильный ответ — второй: 3; 12; 33.
5)
6)
7) Это арифметическая прогрессия.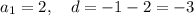
8)
ответ: нет, не является, потому что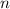
должно быть натуральным числом.
9)
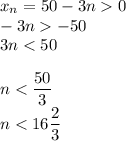
Наибольшее натуральное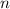
, удовлетворяющее этому неравенству, — это 16.
ответ: 16 членов.
10)
Второе решение не подходит, поскольку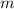
должно быть натуральным числом.
ответ: