Алгебра: Тригонометрия! 4sin4x+sin2x=0

Пояснение:Выражения такого типа, когда в знаменателе сумма или разность числа и числа под корнем, избавляются от иррациональности простым методом. Вспоминаем формулу сокращенного умножения, разность квадратов: . В нашем примере в знаменателе сумма, то есть из формулы. Нам нужно найти и умножить на это дробь, чтобы потом получилось , а , получится просто число, таким образом избавимся от корня в знаменателе. В нашем случае — это , — это . Соответственно, — это .Важно отметить, что нужно умножить...

Тригонометрия!
4sin4x+sin2x=0

Показать ответ

Ответ:

sofira3

10.07.2022 12:07

1) (ab - ac) + (yb - yc) = a(b - c) + y(b -c) = ( b - c)(a +y)
2) ( 3x + 3y) - bx - by = 3(x + y) - b(x + y) = (x+y)(3 - b)
3) (4n - 4) + ( c - nc) = 4( n - 1) + c( 1 - n) = (4 - c)(n - 1)
4) ( x⁷ + x³) - 4x⁴ - 4 = x³(x⁴ + 1) - 4( x⁴ + 1) = (x⁴+1)( x³ - 4)
5) (6mn - 3m) + ( 2n - 1) = 3m( 2n - 1) + ( 2n - 1)=(2n - 1)(3m + 1)
6) (4a⁴ - 8a) +(10y - 5ya³) = 4a(a³ - 2) + 5y(2 - a³) = (4a - 5y)(a³ - 2)
7) a²b² - a + ab² - 1 = (a²b² + ab²) - (a + 1) = ab²(a + 1) - (a+1)=(a+1)(ab² - 1)
8) (xa - xb²) + (zb² - za) - ya + yb² = x(a-b²)+z(b² -a) - y(a -b²)=(x - z - y)(a - b²)

0,0(0 оценок)

Ответ:

rrr46

13.08.2022 01:28

$\frac{1 + \sqrt{x} + x}{1 + \sqrt{x} } = \frac{1 + \sqrt{x} + x }{1 + \sqrt{x} } \times \frac{1 - \sqrt{x} }{1 - \sqrt{x} } = \frac{(1 + \sqrt{x} + x)(1 - \sqrt{x}) }{(1 + \sqrt{x} )(1 - \sqrt{x}) } = \frac{ {1}^{3} - {( \sqrt{x} )}^{3} }{1 - x} = \frac{1 - x \sqrt{x} }{1 - x}$

Пояснение:

Выражения такого типа, когда в знаменателе сумма или разность числа и числа под корнем, избавляются от иррациональности простым методом. Вспоминаем формулу сокращенного умножения, разность квадратов:

${a}^{2} - {b}^{2} = (a - b)(a + b)$ . В нашем примере в знаменателе сумма, то есть (a + b) из формулы. Нам нужно найти (a - b) и умножить на это дробь, чтобы потом получилось ${a}^{2} - {b}^{2}$ , а ${( \sqrt{x} )}^{2} = x$ , получится просто число, таким образом избавимся от корня в знаменателе. В нашем случае — это , — это $\sqrt{x}$ . Соответственно, (a - b) — это $(1 - \sqrt{x} )$ .

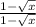Важно отметить, что нужно умножить наше выражение не просто на $(1 - \sqrt{x} )$ , а на $\frac{1 - \sqrt{x} }{1 - \sqrt{x} }$ , потому что $\frac{1 - \sqrt{x} }{1 - \sqrt{x} } = 1$ , а при умножении на 1 значение выражения не измениться. Если умножить просто на $(1 - \sqrt{x} )$ значение выражения поменяется.