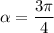Так как в задании не указан метод решения заданного уравнения, то можно применить итерационный метод.
Перенесём второй корень вправо.
∛(8-x) = ∛(x+1) + 3
Методом проб находим, что корень находится между значениями переменной -1 и -2.
х = -1: ∛(8-(-1)) = ∛(-1+1) +3; ∛9 = 3: 2,08 = 3 правая больше.
х = -2 ∛(8-(-2) = ∛(-2+1) + 3; ∛10 = -1+3; 2,15 = 2 правая меньше.
Далее применим подстановку промежуточных значений "х".
Для этого удобно пользоваться программой Excel,
-2 -1,9 -1,8 -1,7 -1,6 -1,5 -1,4 -1,3 -1,2 -1,1 -1
0,15443469 0,112718554 0,068292728 0,020575237 -0,031250196 -0,088387682 -0,152739406 -0,227623332 -0,319817346 -0,448081638 -0,919916177
-1,7 -1,69 -1,68 -1,67 -1,66 -1,65 -1,64 -1,63 -1,62 -1,61 -1,6
0,020575237 0,015593699 0,010570408 0,005504347 0,000394459 -0,004760357 -0,009961247 -0,015209404 -0,020506072 -0,025852552 -0,031250196
-1,66 -1,659 -1,658 -1,657 -1,656 -1,655 -1,654 -1,653 -1,652 -1,651 -1,65
0,000394459 -0,000118982 -0,000632874 -0,001147217 -0,001662013 -0,002177263 -0,002692967 -0,003209128 -0,003725745 -0,004242821 -0,004760357
-1,66 -1,6599 -1,6598 -1,6597 -1,6596 -1,6595 -1,6594 -1,6593 -1,6592 -1,6591 -1,659
0,000394459 0,000343135 0,000291807 0,000240474 0,000189136 0,000137795 8,64481E-05 3,50973E-05 -1,62581E-05 -6,7618E-05 -0,000118982
-1,6593 -1,65929 -1,65928 -1,65927 -1,65926 -1,65925 -1,65924 -1,65923 -1,65922 -1,65921 -1,6592
3,50973E-05 2,99619E-05 2,48266E-05 1,96911E-05 1,45557E-05 9,42015E-06 4,28459E-06 -8,51014E-07 -5,98666E-06 -1,11224E-05 -1,62581E-05.
Более удобное изображение дано во вложении.
С точностью до четвёртого знака х = -1,6592.
Найдем уравнение касательной, проходящей через точку с абсциссой
Для этого найдем производную данной функции:
Найдем значение функции в точке с абсциссой :
Найдем значение производной данной функции в точке с абсциссой :
Уравнение касательной имеет вид:
Подставим значение
Итак, уравнение касательной заданной функции:
Воспользуемся геометрическим смыслом касательной: коэффициент наклона касательной численно равен тангенсу угла наклона с положительным направлением оси
В найденной касательной коэффициент , следовательно, при или
ответ: или
Так как в задании не указан метод решения заданного уравнения, то можно применить итерационный метод.
Перенесём второй корень вправо.
∛(8-x) = ∛(x+1) + 3
Методом проб находим, что корень находится между значениями переменной -1 и -2.
х = -1: ∛(8-(-1)) = ∛(-1+1) +3; ∛9 = 3: 2,08 = 3 правая больше.
х = -2 ∛(8-(-2) = ∛(-2+1) + 3; ∛10 = -1+3; 2,15 = 2 правая меньше.
Далее применим подстановку промежуточных значений "х".
Для этого удобно пользоваться программой Excel,
-2 -1,9 -1,8 -1,7 -1,6 -1,5 -1,4 -1,3 -1,2 -1,1 -1
0,15443469 0,112718554 0,068292728 0,020575237 -0,031250196 -0,088387682 -0,152739406 -0,227623332 -0,319817346 -0,448081638 -0,919916177
-1,7 -1,69 -1,68 -1,67 -1,66 -1,65 -1,64 -1,63 -1,62 -1,61 -1,6
0,020575237 0,015593699 0,010570408 0,005504347 0,000394459 -0,004760357 -0,009961247 -0,015209404 -0,020506072 -0,025852552 -0,031250196
-1,66 -1,659 -1,658 -1,657 -1,656 -1,655 -1,654 -1,653 -1,652 -1,651 -1,65
0,000394459 -0,000118982 -0,000632874 -0,001147217 -0,001662013 -0,002177263 -0,002692967 -0,003209128 -0,003725745 -0,004242821 -0,004760357
-1,66 -1,6599 -1,6598 -1,6597 -1,6596 -1,6595 -1,6594 -1,6593 -1,6592 -1,6591 -1,659
0,000394459 0,000343135 0,000291807 0,000240474 0,000189136 0,000137795 8,64481E-05 3,50973E-05 -1,62581E-05 -6,7618E-05 -0,000118982
-1,6593 -1,65929 -1,65928 -1,65927 -1,65926 -1,65925 -1,65924 -1,65923 -1,65922 -1,65921 -1,6592
3,50973E-05 2,99619E-05 2,48266E-05 1,96911E-05 1,45557E-05 9,42015E-06 4,28459E-06 -8,51014E-07 -5,98666E-06 -1,11224E-05 -1,62581E-05.
Более удобное изображение дано во вложении.
С точностью до четвёртого знака х = -1,6592.
Найдем уравнение касательной, проходящей через точку с абсциссой
Для этого найдем производную данной функции:
Найдем значение функции в точке с абсциссой :
:
Найдем значение производной данной функции в точке с абсциссой :
:
Уравнение касательной имеет вид:
Подставим значение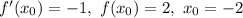
Итак, уравнение касательной заданной функции: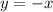
Воспользуемся геометрическим смыслом касательной: коэффициент наклона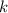 касательной
касательной 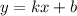 численно равен тангенсу угла наклона
численно равен тангенсу угла наклона 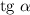 с положительным направлением оси
с положительным направлением оси 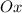
В найденной касательной коэффициент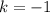 , следовательно,
, следовательно, 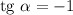 при
при 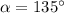 или
или 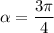
ответ: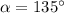 или
или