первое, что хочется предложить для решения системы ---метод подстановки: из одного уравнения выражаешь переменную (любую, например, х = 3+4у) и подставляешь во второе уравнение (вместо х подставляем 3+4у, раскрываем скобки...), получится уравнение относительно одного неизвестного (относительно у) ---оно уже однозначно разрешимо...
а графически решить систему ---это значит построить графики функций (x^2-4x ---парабола, y=x-6 ---прямая линия) и найти точки пересечения графиков ---это и будет решением системы...
первое, что хочется предложить для решения системы ---метод подстановки: из одного уравнения выражаешь переменную (любую, например, х = 3+4у) и подставляешь во второе уравнение (вместо х подставляем 3+4у, раскрываем скобки...), получится уравнение относительно одного неизвестного (относительно у) ---оно уже однозначно разрешимо...
а графически решить систему ---это значит построить графики функций (x^2-4x ---парабола, y=x-6 ---прямая линия) и найти точки пересечения графиков ---это и будет решением системы...
1. берем производную от функции: 3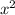
-8x-35
2. приравниваем ее к нулю: 3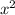
-8x-35=0
д=64+4*3*35=484
х1=(8+22)/6=5 - входит в отрезок [3;12]
х2=(8-22)/6=-14/6 - не входит в отрезок [3;12]
3. теперь в исходную функцию подставляем полученные значения х: 3, 5 и 12 (3 и 12 проверяем так как это концы отрезка)
4. у (3) = 3^3-4*3^2-35*3-16=27-144-105-16 = - 238
y(5) = 5^3-4*5^2-35*5-16 = 125-400-175-16 = -466
y(12) = 12^3-4*12^2-35*12-16 = 1728-2304-420-16= - 742
5/ сравним полученные значения: у (наим) = -742