у квадраті 3x3 клітинки верхня ліва вершина позначена літерою А. Скільки можна побудувати трикутників, однією з вершин яких є точка А, а дві інші вершини - будь-які вершини квадратників 1x1 даного квадрата

Показать ответ

Ответ:

ExplodingPies

18.02.2020 05:08

$3x^2+10x-8\geq 0$

Находим корни уравнения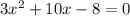 3x^2+10x-8=0 .

$D/4=5^2-3\cdot (-8)=49\ \ ,\ \ \ x_{1,2}=\dfrac{-5\pm 7}{3}\ \ ,\ \ \ x_1=-4\ ,\ x_2=\dfrac{2}{3}$

Дальше можно : либо методом интервалов, либо начертив параболу (схематично) .

1) Метод интервалов.

Раскладываем квадратный трёхчлен на множители.

$3x^2+10x-8=3(x-x_1)(x-x_2)=3(x+4)(x-\frac{2}{3})\\\\3(x+4)(x-\frac{2}{3})\geq 0$

На числовой оси отмечаем нули функции (то есть корни кв. трёхчлена) . Вычисляем знаки на каждом интервале. Нас интересует знак (+), так как знак неравенства " ≥ " .

Знаки: $+++[-4\ ]---[\ \frac{2}{3}\ ]+++$

ответ: $x\in (-\infty \, ;-4\ ]\cup [\ \frac{2}{3}\ ;+\infty \, )$

2) Начертим схематично параболу, учитывая, что ветви её направлены вверх, так как коэффициент при х² равен 3>0 .

И посмотрим, на каких промежутках график лежит выше оси ОХ .

В обоих случаях учитываем , что знак неравенства не строгий, а поэтому корни (нули функции) входят в нужные промежутки .

См. рисунок.

ответ: $x\in (-\infty \, ;-4\ ]\cup [\ \frac{2}{3}\ ;+\infty \, )$ .

Решать всё не нужно просто абъесните как решать на 1 примере. Просто тему не понял ;(

0,0(0 оценок)

Ответ:

evelgren

29.12.2022 15:26

Щоб знайти найбільше та найменьше значення функції нам отрібено знайти її екстремуми, та значення функції у них та кінцях заданого інтервалу

Знвйдемо похіднуфункції

f'(x)=(x^3-3x^2)'=3x^2-6xf′(x)=(x3−3x2)′=3x2−6x

Прирівнюємо похідну к нолю та розвязуємо рівняння

\begin{gathered}3x^2-6x=0\\3x(x-2)=0\\3x=0=\ \textgreater \ x=0\\x-2=0=\ \textgreater \ x=2\end{gathered}3x2−6x=03x(x−2)=03x=0= \textgreater x=0x−2=0= \textgreater x=2

Отримали дві точки: 0 та 2, Накреслити ось Ох, відітити на ній точки 0 та 2, в наслідок чого, ця ось поділиться на три поміжка

1. (- неск;0), 2. [0;2], 3.(2; неск)

Пперевіримо знак похідної на кожному з цих проміжків

1. (- неск;0) -1:3*(-1)^2-6*(-1)=,3*1+6=3+6=9, >0

2. [0;2], 1: 3*1^2-6*1=,3-6=-3, <0

3.(2; неск) 3: 3*3^2-6*3=,3*9-18=27-18=9, >0

Отже юбачимо що точки 0 та 2 є очками екстремуму функції, тепер щоб знайти найбільше та найменше значення подставимо ці точки та кінці проміжку, на якому виконумо обічисленя, у функцію та зннайдемо її значення

\begin{gathered}f(0)=0^3-3*0^2=0-3*0=0\\f(2)=2^3-3*2^2=8-3*4=8-12=-4\\f(3)=3^3-3*3^2=27-3*9=27-27=0\\min_{f(x)}=f(2)=-4, max_{f(x)}=f(0)Uf(3) =0\end{gathered}f(0)=03−3∗02=0−3∗0=0f(2)=23−3∗22=8−3∗4=8−12=−4f(3)=33−3∗32=27−3∗9=27−27=0minf(x)=f(2)=−4,maxf(x)=f(0)Uf(3)=0

Відповідь: найбільше значення функції знаходиться в точках х=0, та х=3 й дорівнює 0, а найменьше значення функції знаходиться в точці х=2 й дорівнює -4

0,0(0 оценок)

Популярные вопросы: Алгебра