Чтобы найти область значения функции, надо сначала найти ординату вершины параболы(n), а для того чтобы найти ординату вершины параболы, надо сначала найти абсциссу вершины параболы по формуле m=- затем подставить вместо х значение m, а потом уже найти n:
m=- =- = - = -4
< br/ > n = f(m) =-8*(-4)+1 = -16+32+1=17
Мы нашли ординату вершины параболы. Это её наибольшее значение. Поэтому все остальные значения параболы будут либо меньше, либо равны 17(≤17).
Поэтому ответ таков: Е(у)=(-∞;17]. Если что, Е(у)- это область значения.
Рассмотрим равнобедренную трапецию АВСД. С углов В и с опустим перпендикуляры ВК и СМ на основание АД. Образовался прямоугольник КВСМ и два прямоугольных треугольника АВК и МСД. Рассмотрим треугольник АВК. Угол АКВ прямой и равен 90 градусов. Угол АВК равен 120 - 90 = 30 градусов. Сторона Ак равна (14 - 8) / 2 = 3 сантиметра. Катет прямоугольного треугольника АВК лежит против угла в 30 градусов, а значит гипотенуза АВ равна 2 * 3 = 6 сантиметров.
ответ: Боковые стороны трапеции равны 6 сантиметров.
Чтобы найти область значения функции, надо сначала найти ординату вершины параболы(n), а для того чтобы найти ординату вершины параболы, надо сначала найти абсциссу вершины параболы по формуле m=-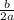
затем подставить вместо х значение m, а потом уже найти n:
m=-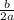
=-
= -
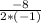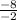= -4
< br/ > n = f(m) =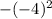
-8*(-4)+1 = -16+32+1=17
Мы нашли ординату вершины параболы. Это её наибольшее значение. Поэтому все остальные значения параболы будут либо меньше, либо равны 17(≤17).
Поэтому ответ таков: Е(у)=(-∞;17]. Если что, Е(у)- это область значения.
УДАЧИ ВАМ ВО ВСЁМ)))!
Объяснение:
Решение задачи:
Рассмотрим равнобедренную трапецию АВСД. С углов В и с опустим перпендикуляры ВК и СМ на основание АД. Образовался прямоугольник КВСМ и два прямоугольных треугольника АВК и МСД. Рассмотрим треугольник АВК. Угол АКВ прямой и равен 90 градусов. Угол АВК равен 120 - 90 = 30 градусов. Сторона Ак равна (14 - 8) / 2 = 3 сантиметра. Катет прямоугольного треугольника АВК лежит против угла в 30 градусов, а значит гипотенуза АВ равна 2 * 3 = 6 сантиметров.
ответ: Боковые стороны трапеции равны 6 сантиметров.