У трикутника АВС АС=2√2 АВ=2√3см
кут В=45°.Знайти градусну міру С​

Я прикрепил фото того, как выглядит график. А сейчас разберемся как его строить.

Для начала давай раскроем скобки:

y = (2x - 6)(x + 1)              //внесли двойку

y = x*(2x - 6) + (2x - 6)    //раскрыли вторую скобку

y = 2x^2 - 6x + 2x - 6

y = 2x^2 - 4x - 6

Теперь можно решать по разному. Если хочешь напишу ещё

А пока воспользуемся самым действенным

Примем x0 и y0 за координаты вершины параболы.

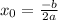Тогда , а 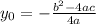(вторую формулу если что можно не запоминать, можешь просто подставить в уравнение полученное x0)

И так

Значит

Теперь может просто подставлять значения. Но в данном случае можешь схитрить.

Так как изначальное уравнение выглядело как y = 2(x - 3)(x + 1), то если присмотреться, то можно заметить, что эта парабола пересекает ось x в точках 3 и -1. Но самое интересное это коэффициент 2. Ты можешь просто квадраты x умножать на два и получать желанную точку. После просмотра второй картинки, мои слова станут более понятны

А) Найдем координаты точек пересечения графика уравнения 3x+5y+15=0 с осями координат.

1. В точке пересечения графика с осью Oy координата x будет равна нулю. Чтобы найти координату y, надо в уравнение вместо x подставить 0 и решить уравнение:

3 * 0 + 5y + 15 = 0;

0 + 5y + 15 = 0;

5y = -15;

y = -15/5;

y = -3.

Точка пересечения графика уравнения с осью Oy имеет координаты (0; -3).

2. Аналогично найдем точку пересечения осью с Ox, подставив 0 вместо y.

3x + 5 *0 + 15 = 0;

3x + 0 + 15 = 0;

3x = -15;

x = -15/3;

x = -5.

Точка пересечения графика уравнения с осью Ox имеет координаты (-5; 0)

Б)Определим, принадлежит ли графику данного уравнения точка С(1/3;-3,2).

Точка будет принадлежать графику уравнения, если подставив координаты точки в уравнение вместо x и y, мы получим верное равенство. Подставим и проверим.

3 * 1/3 + 5 * (-3,2) + 15 = 0;

1 - 16 + 15 = 0;

0 = 0.

Равенство оказалось верным, значит точка С(1/3;-3,2) принадлежит графику