Пусть x - Обрабатываемая площадь посевов в день (ед. измерения - га/день), тогда по норме он должен выполнить заказ ровно за 52/x дней, но известно, что на предыдущий день (т.е на ), он обработал от 48 до 54,6 га, со скоростью, превышающей норму на 3 (т.е скорость равна x+3) итого получаем
поработаем сначала с выражением слева:
52/x - 1 = (52-x)/x, т.е. в Левых частях получается выражение (52-x)(x+3)/x
Раскроем скобки: (-x^2 + 49x + 156)/x
так как x > 0 (Действительно, механизатор не может обрабатывать в отрицательную площадь земли), то можем домножить на x (Обращу внимание, что домножать на x можно ТОЛЬКО если известно, что он только одного знака (в силу одз или условий задачи), причем если x всегда < 0, то нужно еще и поменять знак неравенства):
Нужно было сделать заказ за целое число дней, это означает что 52/x - целое число. Максимально возможное значение 52/x при x=10 52/10=5,2, Минимальное при x=13, 52/13 = 4 т.е. заказ выполнен при норме за 4 или 5 дней, если за 4, то скорость при норме 52/4 = 13 га в день, если за 5 дней, то 52/5 = 10,4 га в день
1) a - (2;1), б - (-2;-1) 2)y = 7x - 8 3) (1/3;1/2);
Объяснение:
1) a) { 3x - 2y = 4 б){ 2x - 7y = 3
{ 5x + 2y = 12 { 3x + 4y = -10
Сложим: Домножим первое уравнение на -1.5
3x+5x-2y+2y=16 {-3x+10,5y=-4,5
8x=16 {3x+4y=-10
x=2 Сложим:
Подставим в первое уравнение: 14,5y = -14,5
3*2 - 2y = 4 y = -1
-2y = 4 - 6 Подставим в первое:
-2y = -2 2x + 7 = 3
y = 1 2x = -4
ответ: (2;1) x=-2
ответ: (-2;-1)
2) Функция проходит через точки (2;6) и (1;-1), а значит можно подставить эти значения в формулу функции:
{6 = 2k+ b
{-1 = 1k + b
Домножим второе на -2:
{6 = 2k+b
{2 = -2k - 2b
Сложим:
6 + 2 = 2k - 2k - 2b + b
-b = 8
b = -8
Подставим в второе уравнение:
-1 = k - 8
k = 7
Получаем функцию: y = 7x-8
3) Сделаем замену 1/x = a; 1/y = b, тогда:
{a + b = 5
{5a - 2b = 11
Умножим первое уравнение на 2:
{2a + 2b = 10
{5a - 2b = 11
Сложим:
2a + 5a + 2b - 2b = 10+11
7a = 21
a = 3
Подставим в первое уравнение:
3 + b = 5
b = 2
Делаем обратную замену:
1/x = 3 1/y = 2
x = 1/3 y = 1/2
10,4 или 13 га в день
Объяснение:
Пусть x - Обрабатываемая площадь посевов в день (ед. измерения - га/день), тогда по норме он должен выполнить заказ ровно за 52/x дней, но известно, что на предыдущий день (т.е на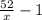
), он обработал от 48 до 54,6 га, со скоростью, превышающей норму на 3 (т.е скорость равна x+3) итого получаем
поработаем сначала с выражением слева:
52/x - 1 = (52-x)/x, т.е. в Левых частях получается выражение (52-x)(x+3)/x
Раскроем скобки: (-x^2 + 49x + 156)/x
так как x > 0 (Действительно, механизатор не может обрабатывать в отрицательную площадь земли), то можем домножить на x (Обращу внимание, что домножать на x можно ТОЛЬКО если известно, что он только одного знака (в силу одз или условий задачи), причем если x всегда < 0, то нужно еще и поменять знак неравенства):
Решим неравенства по отдельности:
1) -x^2 + x + 156 >= 0 2) -x^2-5,6 + 156 <= 0 |*5
D = 1 + 624 = 625 (25*25) -5x^2-28x+780 <= 0
x1 = (-1 - 25)/-2 = 13 D =784 + 15600=16384 (128*128)
x2 = (-1+25)/-2 = -12 x1 = (28-128)/-10 = 10
Далее используя метод x2 = (28+128)/-10 = -15,6
интервалов или свойства Далее используя метод
параболы получаем: интервалов или св-ва параболы:
-12 <= x <= 13 x <= -15,6 или x >= 10
x > 0, следовательно x > 0 следовательно
x <= 13 x >= 10
Нужно было сделать заказ за целое число дней, это означает что 52/x - целое число. Максимально возможное значение 52/x при x=10 52/10=5,2, Минимальное при x=13, 52/13 = 4 т.е. заказ выполнен при норме за 4 или 5 дней, если за 4, то скорость при норме 52/4 = 13 га в день, если за 5 дней, то 52/5 = 10,4 га в день