Дробь является неправильной рациональной дробью, так как степени многочленов в числителе и в знаменателе одинаковые и равны 1. Значит можно выделить целую и дробную часть неправильной дроби. Так как в знаменателе стоит многочлен 1 степени (линейная ф-ция) х+1, то и в числителе выделим х+1. Для этого надо вынести за скобки коэффициент (-5), который стоит перед х, и записать в скобках (х+1). Так как -5(х+1)=-5х-5, то , чтобы выражение не изменилось, надо добавить (+5), получим:
.
Если в дальнейшем надо записать целую и дробную части неправильной рац. дроби, то
Три брата, возраст которых образует геометрическую прогрессию, делят между собой некую сумму денег пропорционально своему возрасту. Если бы они это проделали через 3 года, когда самый младший окажется вдвое моложе самого старшего, то младший получил бы на 105, а средний на 15 рублей больше, чем сейчас. Сколько лет каждому из братьев? Решение: Пусть братьям a,aq и aq2 лет. Тогда они получат соответственно x,xq и xq2 рублей. Через 3 года им будет a+3,aq+3 и aq2+3 лет, причем старшему окажется вдвое больше лет, чем младшему: aq2+3=2(a+3) (1). При дележе через 3 года младший брат получит x+105, средний xq+15. Чтобы узнать, сколько получит старший брат, вычтем эти деньги из всей суммы: x+xq+xq2−(x+105)−(xq+15)=xq2−120. Так как братья делят деньги пропорционально их возрасту, то получим еще два уравнения: x+105a+3=xq+15aq+3,x+105a+3=xq2−120aq2+3 (2). Уравнение (1) позволяет записать второе из уравнений (2) так: 2(x+105)=xq2−120, т. е. x(q2−2)=3. (3) Если в (1) раскрыть скобки, а затем вынести за скобки a, то a(q2−2)=3. (1') Сравним с уравнением (3): x=110a. Первое из уравнений (2) можно переписать так: (110a+105)(aq+3)=(110aq+15)(a+3). Раскроем скобки и решим систему, состоящую из уравнения, полученного в результате, и из уравнения (1'): {5aq−7a=6a(q2−2)=3. Из первого уравнения a=65q−7. Подставим во второе. После преобразований получим квадратное уравнение 6q2−15q+9=0, откуда q1=32,q2=1. Второй корень посторонний, так как тогда всем братьям одинаковое количество лет и никто из них не может через 3 года стать вдвое старше другого. ответ. 12, 18, 27.
Дробь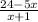 является неправильной рациональной дробью, так как степени многочленов в числителе и в знаменателе одинаковые и равны 1. Значит можно выделить целую и дробную часть неправильной дроби. Так как в знаменателе стоит многочлен 1 степени (линейная ф-ция) х+1, то и в числителе выделим х+1. Для этого надо вынести за скобки коэффициент (-5), который стоит перед х, и записать в скобках (х+1). Так как -5(х+1)=-5х-5, то , чтобы выражение не изменилось, надо добавить (+5), получим:
является неправильной рациональной дробью, так как степени многочленов в числителе и в знаменателе одинаковые и равны 1. Значит можно выделить целую и дробную часть неправильной дроби. Так как в знаменателе стоит многочлен 1 степени (линейная ф-ция) х+1, то и в числителе выделим х+1. Для этого надо вынести за скобки коэффициент (-5), который стоит перед х, и записать в скобках (х+1). Так как -5(х+1)=-5х-5, то , чтобы выражение не изменилось, надо добавить (+5), получим:
Если в дальнейшем надо записать целую и дробную части неправильной рац. дроби, то
Три брата, возраст которых образует геометрическую прогрессию, делят между собой некую сумму денег пропорционально своему возрасту. Если бы они это проделали через 3 года, когда самый младший окажется вдвое моложе самого старшего, то младший получил бы на 105, а средний на 15 рублей больше, чем сейчас. Сколько лет каждому из братьев? Решение: Пусть братьям a,aq и aq2 лет. Тогда они получат соответственно x,xq и xq2 рублей. Через 3 года им будет a+3,aq+3 и aq2+3 лет, причем старшему окажется вдвое больше лет, чем младшему: aq2+3=2(a+3) (1). При дележе через 3 года младший брат получит x+105, средний xq+15. Чтобы узнать, сколько получит старший брат, вычтем эти деньги из всей суммы: x+xq+xq2−(x+105)−(xq+15)=xq2−120. Так как братья делят деньги пропорционально их возрасту, то получим еще два уравнения: x+105a+3=xq+15aq+3,x+105a+3=xq2−120aq2+3 (2). Уравнение (1) позволяет записать второе из уравнений (2) так: 2(x+105)=xq2−120, т. е. x(q2−2)=3. (3) Если в (1) раскрыть скобки, а затем вынести за скобки a, то a(q2−2)=3. (1') Сравним с уравнением (3): x=110a. Первое из уравнений (2) можно переписать так: (110a+105)(aq+3)=(110aq+15)(a+3). Раскроем скобки и решим систему, состоящую из уравнения, полученного в результате, и из уравнения (1'): {5aq−7a=6a(q2−2)=3. Из первого уравнения a=65q−7. Подставим во второе. После преобразований получим квадратное уравнение 6q2−15q+9=0, откуда q1=32,q2=1. Второй корень посторонний, так как тогда всем братьям одинаковое количество лет и никто из них не может через 3 года стать вдвое старше другого. ответ. 12, 18, 27.
Объяснение:
ответ. 12, 18, 27.