Практически очевидно, что если сумма квадратов двух положительных чисел меньше 100, то сумма самих этих чисел не может быть больше 64. Докажем это строго.
Первый
Пусть сумма квадратов двух положительных чисел х и у равна 100.
Составим выражение для суммы чисел х и у и найдем при каком условии оно принимает максимальное значение и чему равно это значение.
Выразим у из первого условия:
Найдем производную:
Найдем точки экстремума:
Учитывая, что х - положительное:
- точка максимума
Максимум достигается при и он равен:
Итак, даже при условии, что сумма квадратов равна 100, сама сумма не может быть больше . По условию сумма квадратов меньше 100, значит сумма самих чисел меньше и точно не может быть больше 64. Значит, искомая вероятность равна 0.
Второй
Графически решить систему и найти отношение площади фигуры, соответствующей решению этой системы, к площади, являющейся решением системы (четверть окружности радиуса 10). Однако, первая система решений иметь не будет, значит вероятность равна 0.
Практически очевидно, что если сумма квадратов двух положительных чисел меньше 100, то сумма самих этих чисел не может быть больше 64. Докажем это строго.
Первый
Пусть сумма квадратов двух положительных чисел х и у равна 100.
Составим выражение для суммы чисел х и у и найдем при каком условии оно принимает максимальное значение и чему равно это значение.
Выразим у из первого условия: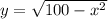
Найдем производную:
Найдем точки экстремума:
Учитывая, что х - положительное:
Максимум достигается при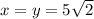 и он равен:
и он равен:
Итак, даже при условии, что сумма квадратов равна 100, сама сумма не может быть больше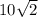 . По условию сумма квадратов меньше 100, значит сумма самих чисел меньше
. По условию сумма квадратов меньше 100, значит сумма самих чисел меньше 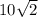 и точно не может быть больше 64. Значит, искомая вероятность равна 0.
и точно не может быть больше 64. Значит, искомая вероятность равна 0.
Второй
Графически решить систему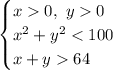 и найти отношение площади фигуры, соответствующей решению этой системы, к площади, являющейся решением системы
и найти отношение площади фигуры, соответствующей решению этой системы, к площади, являющейся решением системы 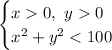 (четверть окружности радиуса 10). Однако, первая система решений иметь не будет, значит вероятность равна 0.
(четверть окружности радиуса 10). Однако, первая система решений иметь не будет, значит вероятность равна 0.
ответ: 0