У выражение
С пошаговым решением

Функция является возрастающей, если для любых двух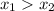 , принадлежащих области определения функции, выполняется неравенство .

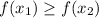Если же мы рассматриваем строго возрастающую функцию, то последнее неравенство обязано быть строгим.

Также говорят, что функция является возрастающей, если большему значению аргумента соответствует большее значение функции.  

Пример: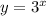 (розовый график ниже) - [строго] возрастающая функция.

Функция является убывающей, если для любых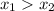 из области определения верно обратное неравенство: .

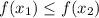Если имеем дело со строго убывающей функцией, то знак "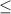" нужно заменить на знак "".

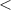Также говорят, что функция является убывающей, если большему значению аргумента соответствует меньшее значение функции.

Пример: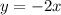 (зеленый график ниже) - [строго] убывающая функция.

25x-2x+2+9xx+2=56xx-2 
Перенесем все в левую часть.
25x-2x+2+9xx+2-56xx-2=0 
25x-2x+2+9xx+2-56xx-2=0 
Раскрываем скобки.
25x-50x+2+9x2+18x-56x2-112x=0 
Раскрываем скобки.
25x2+50x-50x-100+9x2+18x-56x2-112x=0 
Приводим подобные члены.
25x2-100+9x2+18x-56x2-112x=0 
Раскрываем скобки.
25x2-100+9x2+18x-56x2+112x=0 
Приводим подобные члены.
-22x2-100+130x=0 
Изменяем порядок действий.
-22x2+130x-100=0 
Изменим знаки выражений на противоположные.
22x2-130x+100=0 
Следующее уравнение равносильно предыдущему.
11x2-65x+50=0 
Находим дискриминант.
D=b2-4ac=-652-4•11•50=2025 
Дискриминант положителен, значит уравнение имеет два корня.
Воспользуемся формулой корней квадратного уравнения.
x1,2=-b±D2a 
x1=65-452•11=1011 ;x2=65+452•11=5 
x=1011;x=5 . ответ: 5 км в час