Есть правило: Бесконечная периодическая десятичная дробь равна обыкновенной дроби, в числителе которой разность между всем числом после запятой и числом после запятой до периода, а знаменатель состоит из «девяток» и «нулей», причем, «девяток» столько, сколько цифр в периоде, а «нулей» столько, сколько цифр после запятой до периода.
В первом примере
1) 0, (3). В числителе обыкновенной дроби запишем разность между всем числом после запятой (3) и числом после запятой до периода дроби (0). В периоде одна цифра, а после запятой до периода ни одной, поэтому знаменатель будет состоять из одной девятки (9).
0, 2(5). В числителе обыкновенной дроби запишем разность между всем числом после запятой (25) и числом после запятой до периода дроби (2). В периоде одна цифра, а после запятой до периода одна, поэтому знаменатель будет состоять из одной девятки и одного нуля (90).
7,(36)В числителе обыкновенной дроби запишем разность между всем числом после запятой (36) и числом после запятой до периода дроби (0). В периоде две цифры, а после запятой до периода ни одной, поэтому знаменатель будет состоять из двух девяток (99).
из всех правил сдвига графика функций, я выберу те, которые касаются нашей функции
1. если ФУНКЦИЯ умножается на число 0<m<1 , то происходит сжатие её графика вдоль оси oy в 1/m раз
2. если АРГУМЕНТ функции умножается на 0<k<1, то график функции растягивается от оси оу в 1/k раз
3. если к АРГУМЕНТУ функции добавляется константа b y(x+b), то происходит сдвиг (параллельный перенос) графика вдоль оси оx на b единиц влево .
теперь проделаем все это с нашей функцией
начнем с простого
1. у нас ФУНКЦИЯ умножается на число 0< 1/4 <1, значит мы будем сжимать функцию y = cos(x) в 4 раза вдоль оси оу
2. у нас АРГУМЕНТ функции умножается на 0< 1/2 <1, значит мы будем растягивать график у = cos(x) от оси оу в 2 раза
3. а вот теперь тут будет не так просто. поскольку правило 3 справедливо для графика функции y(x+b), нам надо привести свою заданную функцию к такому виду
таким образом у нас будет сдвиг (параллельный перенос) графика
9,90,99
Объяснение:
Сумма бесконечно убывающей геометрической прогрессии:
Есть правило: Бесконечная периодическая десятичная дробь равна обыкновенной дроби, в числителе которой разность между всем числом после запятой и числом после запятой до периода, а знаменатель состоит из «девяток» и «нулей», причем, «девяток» столько, сколько цифр в периоде, а «нулей» столько, сколько цифр после запятой до периода.
В первом примере
1) 0, (3). В числителе обыкновенной дроби запишем разность между всем числом после запятой (3) и числом после запятой до периода дроби (0). В периоде одна цифра, а после запятой до периода ни одной, поэтому знаменатель будет состоять из одной девятки (9).
0, 2(5). В числителе обыкновенной дроби запишем разность между всем числом после запятой (25) и числом после запятой до периода дроби (2). В периоде одна цифра, а после запятой до периода одна, поэтому знаменатель будет состоять из одной девятки и одного нуля (90).
7,(36)В числителе обыкновенной дроби запишем разность между всем числом после запятой (36) и числом после запятой до периода дроби (0). В периоде две цифры, а после запятой до периода ни одной, поэтому знаменатель будет состоять из двух девяток (99).
Объяснение:
из всех правил сдвига графика функций, я выберу те, которые касаются нашей функции
1. если ФУНКЦИЯ умножается на число 0<m<1 , то происходит сжатие её графика вдоль оси oy в 1/m раз
2. если АРГУМЕНТ функции умножается на 0<k<1, то график функции растягивается от оси оу в 1/k раз
3. если к АРГУМЕНТУ функции добавляется константа b y(x+b), то происходит сдвиг (параллельный перенос) графика вдоль оси оx на b единиц влево .
теперь проделаем все это с нашей функцией
начнем с простого
1. у нас ФУНКЦИЯ умножается на число 0< 1/4 <1, значит мы будем сжимать функцию y = cos(x) в 4 раза вдоль оси оу
2. у нас АРГУМЕНТ функции умножается на 0< 1/2 <1, значит мы будем растягивать график у = cos(x) от оси оу в 2 раза
3. а вот теперь тут будет не так просто. поскольку правило 3 справедливо для графика функции y(x+b), нам надо привести свою заданную функцию к такому виду
таким образом у нас будет сдвиг (параллельный перенос) графика
у = cos(x) вдоль оси оx на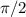
единиц влево
ну и вот что должно получиться.