Укажіть нерівність, що є лінійною нерівністю з однією змінною.
А. 7-1> 10 Б. 7х35 в. 3х2 > 12 г.
1
30
3х+6
3. Розв'яжіть нерівність :
1) - 6x > 18
2) 9x - 22x+14
4. Відомо, що 3 < x < 8 і 2<y<7. Оцініть значення виразу :
1) x+y 2) х - у 3) xy 4) *
y
5. Розв'язати систему нерівностей:
1) бх – 24 >0, 2) 2x +7<19,
- 2x +12 0 30 – 8x < 6
1) *+14
6. Розв'яжіть нерівність:
х+14 x-12
<3
8
4 - 5x
2) – 35
1
2
7. Знайти цілі розв'язки системи нерівностей:
(2(3х – 4) = 4(х+1) - 3
х(х – 4)- (х+3)(х – 5)> -5
8. Знайдіть допустимі значення змінних:
1) 3х – 5
1
2) 3х – 9+
40 - 5x
9. Доведіть, що при всіх дійсних значеннях змінних є правильною
нерівність 10х? – 6xy +y? - 4х +6> 0
них є правильною

Показать ответ

Ответ:

MaxWatt

25.11.2022 02:25

Школьные Знания.com

Какой у тебя вопрос?

Sabina05 avatar

Sabina05

21.02.2012

Алгебра

5 - 9 классы

ответ дан • проверенный экспертом

периметр прямоугольника равен 22 см, а его площадь равна 30см (в квадрате) Найдите стороны прямоугольника

ПОСМОТРЕТЬ ОТВЕТЫ

ответ, проверенный экспертом

4,0/5

Svet1ana

главный мозг

4.2 тыс. ответов

8.4 млн пользователей, получивших

а - длина прямоугольника

b - ширина прямоугольника

Р=22 см

S=30 см²

а - ? см

b - ? см

(1)

(2)

из формулы площади прямоугольника (2) выводим формулу нахождения ширины

подставляем в формулу периметра прямоугольника (1)

/·a

умножаем на а для того, чтобы избавиться от знаменателя

подставим в уравнение данные P и S

Квадратное уравнение имеет вид:

Считаем дискриминант:

Дискриминант положительный

Уравнение имеет два различных корня:

Следовательно, стороны равны 6см и 5см соответственно

ответ: 6см и 5см стороны прямоугольника.

Проверка:

Р=2(а+b)=2(6+5)=2·11=22 (см)

S=a·b=6·5=30 (м²)

Объяснение:

0,0(0 оценок)

Ответ:

jhghjlkuyfjy

11.07.2020 05:30

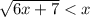
1) $\sqrt{6x+7} < x$

Составим систему неравенств, учитывая каждое ограничение, накладывающееся на аргумент:

$\begin{equation*}\begin{cases}6x + 7 \geq 0\\x \geq 0\end{cases}\end{equation*}\ \ \ \Leftrightarrow\ \begin{equation*}\begin{cases}x \geq -\dfrac{7}{6}\\\\x \geq 0\end{cases}\end{equation*}\ \ \ \ \ \Rightarrow\ \boxed{x\geq 0}$

Теперь продолжаем решать наше неравенство.

$\sqrt{6x+7} < x$

Возведём обе части неравенства в квадрат.

$6x + 7 < x^2\\\\-x^2 + 6x + 7 < 0\ \ \ \ \ \Big| \cdot (-1)\\\\x^2 - 6x - 7 0$

Получаем квадратное неравенство. Чтобы найти нули, приравняем левую часть к 0 и найдём корни квадратного уравнения.

x^2 - 6x - 7 = 0

По теореме Виета:

$\begin{equation*}\begin{cases}x_{1}x_{2} = -7\\x_{1} + x_{2} = 6\end{cases}\end{equation*}\ \ \ \ \ \Big| x = 7; x = -1$

Возвращаемся к неравенству:

(x-7)(x+1) 0

Решим его методом интервалов.

Нули: 7; -1.

+ - +

---------------------о------------------------------о-----------------------> х

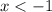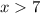Получаем, что решением квадратного неравенства являются промежутки x < -1 и x 7 . Но не забываем про ограничение 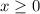$x \geq 0$ , которое мы вычислили выше.

$\begin{equation*}\begin{cases}x\geq 0\\$\left[\begin{gathered}x < -1\\x 7\end{gathered}\end{cases}\end{equation*}\ \ \ \ \Rightarrow\ \boxed{x 7}$

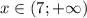ответ: $x \in (7;+\infty)$ .

2) $(x-2)^2(x^2-4x+3)\geq 0$

Это задание можно решить методом интервалов. Нужно найти нули. С левым множителем понятно, он обращается в 0 при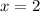 x = 2 . Приравняем правый множитель к нулю, чтобы найти его корни.

x^2 - 4x + 3 = 0

По теореме Виета:

$\begin{equation*}\begin{cases}x_{1}x_{2} = 3\\x_{1} + x_{2} = 4\end{cases}\end{equation*}\ \ \ \ \ \Big| x = 3; x = 1$

Применяем метод интервалов для нашего неравенства.

$(x-2)^2(x-3)(x-1) \geq 0$

Нули: 1; 2; 3.

+ - - +

--------------- $\bullet$ --------------------- $\bullet$ --------------------- $\bullet$ -------------------> x

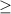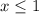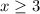Так как знак неравенства $\geq$ , то нам нужны те промежутки где стоит знак +. Таких два: $x \leq 1$ и $x \geq 3$ , но и это ещё не всё. Есть ещё точка 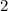, и она тоже является решением, поскольку при ней выражение обращается в 0.