Укажи для каждой функции, записанной в левом столбце, точку, записанную в правом столбце, через которую проходит график этой функции. у = 3х - 5 у = -2 y = 14 - 6x y= -1/16x y=1/11x+11
Обоснование. Как известно, число делится на 11 тогда и только тогда, когда сумма цифр, стоящих на нечетных местах, отличается от суммы цифр, стоящих на четных, на число, делящееся на 11 (как частный случай эти суммы могут совпадать). Однако в нашем случае максимальное возможное отличие равно 8 (из двузначных это число 19, из трехзначных 129, 239, ..., 789). Докажем, что больше 8 никогда не получится.
1) Пусть в числе четное число знаков: Тогда
- это часть расстояния от до , а поскольку первая цифра не меньше 1, а последняя не больше 9, эта сумма не больше 8.
2) Пусть в числе нечетное число знаков: Тогда
то есть из вычитается часть расстояния между и
Поэтому снова больше 8 получиться не может.
Но одновременно мы видим, что 0 также не может получиться.
Вывод: число, у которого цифры идут в порядке возрастания, на 11 делиться не может.
ответ: делиться на 11 такое число не может.
Обоснование. Как известно, число делится на 11 тогда и только тогда, когда сумма цифр, стоящих на нечетных местах, отличается от суммы цифр, стоящих на четных, на число, делящееся на 11 (как частный случай эти суммы могут совпадать). Однако в нашем случае максимальное возможное отличие равно 8 (из двузначных это число 19, из трехзначных 129, 239, ..., 789). Докажем, что больше 8 никогда не получится.
1) Пусть в числе четное число знаков: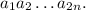
Тогда
2) Пусть в числе нечетное число знаков: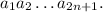
Тогда
то есть из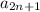
вычитается часть расстояния между 
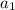и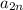 
Поэтому снова больше 8 получиться не может.
Но одновременно мы видим, что 0 также не может получиться.
Вывод: число, у которого цифры идут в порядке возрастания, на 11 делиться не может.
Объяснение:
Было число:
X = 1000a + 100b + 10c + d
У него поменяли первую и последнюю цифры, стало:
Y = 1000d + 100b + 10c + a
Потом эти два числа сложили, получилось:
X + Y = 1001a + 200b + 20c + 1001d
И оно делится на 91 = 7*13. Выделим числа, кратные 91, и найдем остаток.
Заметим, что 1001 = 7*11*13 = 91*11, поэтому 1001а и 1001d кратны 91.
X + Y = 91*11a + 91*11d + 91*2b + 18b + 20c
Остаток от деления на 91 равен 18b + 20c. И этот остаток тоже должен делиться на 91.
Так как b и с - однозначные цифры, то 18b + 20c ≤ 18*8+20*9 = 324.
К тому же, число 18b + 20c - четное, и может равняться только 91*2=182.
18b + 20c = 182
9b + 10c = 91.
b = 9; c = 1; 9b + 10c = 9*9 + 10*1 = 91
Это решение - единственное.
Значит, число имело вид:
X = 1000a + 910 + d
Нам надо доказать, что оно НЕ делится на 91.
Ясно, что 910 делится на 91.
Число X может делиться на 91, только если 1000a + d делится на 91.
А это возможно, только если это числа вида: 1001; 2002; ...; 9009.
Во всех случаях a = d, но это неправильно: по условию мы взяли число из 4 разных цифр.
Таким образом, мы доказали, что число
X = 1000a + 100b + 10c + d
Не может быть кратно 91, при заданных в задаче условиях.