Укажи степень данного уравнения х^3у^2+2ху-7х^4у=0

Задать вопрос

Войти

АнонимГеометрия13 мая 17:10

треугольник MNP равнобедренный. один из углов равен 112 градусам. найти углы

ответ или решение1

Боброва Кира

Рассмотрим два возможный случая.

1 случай.

Данный угол величиной 112° является углом при вершине данного равнобедренного треугольника.

Тогда два других угла при основании будут равны между собой.

Обозначим через x величину этих углов.

Так как при сложении величин всех трех углов всякого треугольника в результате получается 180°, можем составить следующее уравнение:

х + х + 112 = 180,

решая которое, получаем:

2х + 112 = 180;

(2х + 112) / 2 = 180 / 2;

х + 56 = 90;

х = 90 - 56 = 34°.

2 случай.

Данный угол величиной 112° является углом при основании данного равнобедренного треугольника.

Тогда другой угол при основании также должен составлять 112°.

Так как суммы этих двух углов, равная 112 + 112 = 224° больше 180°, то такого треугольника не существует.

ответ: 112°, 54°, 54°.

Для решения запишем формулу бинома Ньютона:

Если а - слагаемое, содержащее неизвестную в наибольшей степени, то для определения степени результата нужно рассмотреть выражение .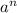

Если b - слагаемое, не содержащее неизвестную, то для определения свободного члена результата нужно рассмотреть выражение .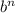

Рассмотрим многочлен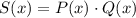 , где:

Для определения степени и свободного члена произведения достаточно знать степень и свободный член каждого из множителей.

Для многочлена :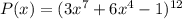

- степень определяется выражением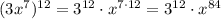 , то есть степень равна 84

- свободный член равен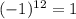

Для многочлена :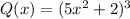

- степень определяется выражением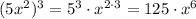 , то есть степень равна 6

- свободный член равен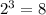

Наконец, для многочлена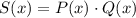 получим:

- степень определяется выражением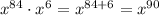 , то есть степень равна 90

- свободный член равен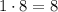

Сумма степени и свободного члена многочлена :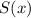

ответ: 98