Обратившись к основному тригонометрическому тождеству, получим:
2sin^2(x) - 5sin(x)cos(x) + 5cos^2(x) = sin^2(x) + cos^2(x);
sin^2(x) - 5sin(x)cos(x) + 4cos^(x) = 0.
Разделим полученное уравнение на cos^2(x):
tg^2(x) - 5tg(x) + 4 = 0.
Произведем замену переменных t = tg(t):
t^2 - 5t + 4 = 0.
Корни квадратного уравнения вида ax^2 + bx + c = 0 определяются
по формуле: x12 = (-b +- √(b^2 - 4 * a * c) / 2 * a.
t12 = (5 +- 3) / 2;
t1 = 1; t2 = 4.
tg(x) = 1;
x1 = π/4 +- π * n.
x2 = arctg(4) +- π * n.
Объяснение:
Пусть за час 1-й кран будет наполнять весь бассейн
за час 2-й кран будет наполнять бассейн.
Если 1 - это объем всего бассейна, тогда
- объем воды, который проходит через 1-й кран за 1 час.
- объем воды, который проходит через 2-й кран за 1 час.
- общая производительность двух кранов.
- первое уравнение
- второе уравнение
Из первого уравнения получим: и вставим во второе уравнение:
Подставим в первое уравнение:
ответ: за 3 часа 1-й кран наполнит весь бассейн;
за 6 часов 2-й кран наполнит весь бассейн.
Обратившись к основному тригонометрическому тождеству, получим:
2sin^2(x) - 5sin(x)cos(x) + 5cos^2(x) = sin^2(x) + cos^2(x);
sin^2(x) - 5sin(x)cos(x) + 4cos^(x) = 0.
Разделим полученное уравнение на cos^2(x):
tg^2(x) - 5tg(x) + 4 = 0.
Произведем замену переменных t = tg(t):
t^2 - 5t + 4 = 0.
Корни квадратного уравнения вида ax^2 + bx + c = 0 определяются
по формуле: x12 = (-b +- √(b^2 - 4 * a * c) / 2 * a.
t12 = (5 +- 3) / 2;
t1 = 1; t2 = 4.
tg(x) = 1;
x1 = π/4 +- π * n.
x2 = arctg(4) +- π * n.
Объяснение:
Пусть за
час 1-й кран будет наполнять весь бассейн
за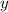
час 2-й кран будет наполнять бассейн.
Если 1 - это объем всего бассейна, тогда
Из первого уравнения получим: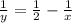
и вставим во второе уравнение:
Подставим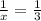
в первое уравнение:
ответ: за 3 часа 1-й кран наполнит весь бассейн;
за 6 часов 2-й кран наполнит весь бассейн.