Для начала вспомним что такое область определения и область значения: - Область определения D(f) это множество допустимых значений независимой переменной x. - Область значений E(f) это множество, которое пробегает зависимая переменная y, когда переменная x пробегает область определения D(f).
У нашей функции область определения это множество натуральных чисел. Натуральные числа это числа, возникающие естественным образом при счёте (например, 1, 2, 3, 4, 5…).
Область значений образуется значением числа единиц в записи куба натурального числа
попробуем на примере составить такие значения для первых значений х
Экстремумы на отрезке находятся либо в стационарных точках (точках, где производная функции обращается в ноль), либо на концах отрезка.
Для этого сначала нужно найти производную функции. Если я правильно поняла запись Вашей функции и она такая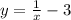
То ее производная равна -1/х^2
Критической точкой здесь будет х=0. Но наша функция в этой точке не существует. Значит экстремумы находятся на концах отрезка:
у(-1)=-4
у(1)=-2
Значит минимальное значение функция достигает в точке х=-1 и равна -4.
Максимальное значение функции на отрезке равно -2 и находится в точке х=1.
- Область определения D(f) это множество допустимых значений независимой переменной x.
- Область значений E(f) это множество, которое пробегает зависимая переменная y, когда переменная x пробегает область определения D(f).
У нашей функции область определения это множество натуральных чисел.
Натуральные числа это числа, возникающие естественным образом при счёте (например, 1, 2, 3, 4, 5…).
Область значений образуется значением числа единиц в записи куба натурального числа
попробуем на примере составить такие значения для первых значений х
х 1 2 3 4 5 6 7 8 9 10
х³ 1 8 27 64 125 216 343 512 729 1000
у 1 8 7 4 5 6 3 2 9 0
Как мы видим у принимает значения 0;1;2;3;4;5;6;7;8;9
Значит областью значений нашей функции будут точки {0;1;2;3;4;5;6;7;8;9}