Число даёт остаток 1 при делении на 2017 — это значит, что оно почти делится на 2017, просто у него есть лишняя единичка. То есть число a можно представить, как a = 2017p + 1 (p — это какое-то натуральное число). То же самое можно сказать и про 2018: a = 2018q + 1 (опять же, q — натуральное число). Получаем:
a = 2017p + 1
a = 2018q + 1
Левые части равны, значит, правые тоже должны быть равны:
2017p + 1 = 2018q + 1
2017p = 2018q
Чтобы найти наименьшее a, необходимо найти либо наименьшее возможное p, либо наименьшее возможное q и подставить в одно из уравнений.
Левая часть последнего уравнения делится на 2017 (потому что там есть множитель 2017), значит, и правая тоже делится на 2017. Но 2018 не имеет общих множителей с 2017 (то есть взять какие-то общие части из 2017 и 2018 нельзя, так как НОД(2017, 2018) = 1 — НОД соседних чисел всегда равен 1). Тогда на 2017 будет делиться q, а наименьшее q, которое делится на 2017 — это само q = 2017 (вообще 0 тоже делится на 2017, но если взять q = 0, то a = 1, что не удовлетворяет условию). Получаем a = 2018q + 1 = 2018·2017 + 1.
В ответе нужно указать остаток от деления на 5. Вспомним признак делимости на 5: если число оканчивается на 5 или на 0, то оно делится на 5. Значит, если оно даёт какой-то остаток при делении на 5, появляются лишние "добавочки", и последняя цифра увеличится на этот остаток.
Проверим последнюю цифру числа a: __7·__8 + 1 = __6 + 1 = __7. Последняя цифра 7. Она отличается от 5 на 2, значит, и остаток тоже будет равен двум.
Параллельная прямая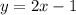
, перпендикулярная прямая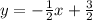 
Объяснение:
Перепишем уравнение прямой в виде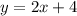
.
Тогда прямая, параллельная данной, имеет тот же угловой коэффициент, то есть записывается в виде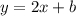
.
Так как эта прямая проходит через точку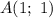
, эти координаты должны удовлетворять этому уравнению:
Значит искомое уравнение параллельной прямой: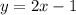
.
Угловые коэффициенты перпендикулярных прямых в произведении дают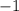
. Поэтому уравнение прямой, перпендикулярной данной, записывается в виде
Так как и эта прямая проходит через точку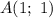
, эти координаты должны удовлетворять этому уравнению:
Значит искомое уравнение перпендикулярной прямой:
b) 2
Объяснение:
Число даёт остаток 1 при делении на 2017 — это значит, что оно почти делится на 2017, просто у него есть лишняя единичка. То есть число a можно представить, как a = 2017p + 1 (p — это какое-то натуральное число). То же самое можно сказать и про 2018: a = 2018q + 1 (опять же, q — натуральное число). Получаем:
a = 2017p + 1
a = 2018q + 1
Левые части равны, значит, правые тоже должны быть равны:
2017p + 1 = 2018q + 1
2017p = 2018q
Чтобы найти наименьшее a, необходимо найти либо наименьшее возможное p, либо наименьшее возможное q и подставить в одно из уравнений.
Левая часть последнего уравнения делится на 2017 (потому что там есть множитель 2017), значит, и правая тоже делится на 2017. Но 2018 не имеет общих множителей с 2017 (то есть взять какие-то общие части из 2017 и 2018 нельзя, так как НОД(2017, 2018) = 1 — НОД соседних чисел всегда равен 1). Тогда на 2017 будет делиться q, а наименьшее q, которое делится на 2017 — это само q = 2017 (вообще 0 тоже делится на 2017, но если взять q = 0, то a = 1, что не удовлетворяет условию). Получаем a = 2018q + 1 = 2018·2017 + 1.
В ответе нужно указать остаток от деления на 5. Вспомним признак делимости на 5: если число оканчивается на 5 или на 0, то оно делится на 5. Значит, если оно даёт какой-то остаток при делении на 5, появляются лишние "добавочки", и последняя цифра увеличится на этот остаток.
Проверим последнюю цифру числа a: __7·__8 + 1 = __6 + 1 = __7. Последняя цифра 7. Она отличается от 5 на 2, значит, и остаток тоже будет равен двум.