Для розв'язання системи рівнянь методом підстановки, спочатку виразимо одну змінну через іншу в одному з рівнянь, а потім підставимо це значення в друге рівняння.
1. Виразимо х через у з першого рівняння:
х = 3 + 2у
2. Підставимо це значення х у друге рівняння:
5(3 + 2у) + у = 4
3. Розкриємо дужки і спростимо рівняння:
15 + 10у + у = 4
11у + 15 = 4
11у = 4 - 15
11у = -11
у = -11 / 11
у = -1
4. Тепер, коли ми знайшли значення у, підставимо його у перше рівняння для знаходження х:
х = 3 + 2(-1)
х = 3 - 2
х = 1
Отже, розв'язком системи рівнянь є х = 1 і у = -1.
Для розв'язання системи рівнянь методом підстановки, спочатку виразимо одну змінну через іншу в одному з рівнянь, а потім підставимо це значення в друге рівняння.
1. Виразимо х через у з першого рівняння:
х = 3 + 2у
2. Підставимо це значення х у друге рівняння:
5(3 + 2у) + у = 4
3. Розкриємо дужки і спростимо рівняння:
15 + 10у + у = 4
11у + 15 = 4
11у = 4 - 15
11у = -11
у = -11 / 11
у = -1
4. Тепер, коли ми знайшли значення у, підставимо його у перше рівняння для знаходження х:
х = 3 + 2(-1)
х = 3 - 2
х = 1
Отже, розв'язком системи рівнянь є х = 1 і у = -1.
наибольшее значение функции равно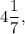 а наименьшее значение функции равно
а наименьшее значение функции равно 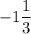
Объяснение:
Найти наибольшее и наименьшее значение функции
Так как делить на нуль нельзя, то 2х -3 ≠0, то есть х ≠ 1,5.
Тогда область определение функции: D(y) = ( -∞ ; 1,5 ) ∪(1,5; + ∞)
Найдем производную функции
Найдем критические точки, решив уравнение: y' = 0.
Дробь равна нулю, если числитель равен нулю
Заданному промежутку [ 0; 5] принадлежит х =4.
Найдем значение функции на концах промежутка и в точке х =4 .
Сравним найденные значения и получим, что наибольшее значение функции равно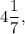 а наименьшее значение функции равно
а наименьшее значение функции равно 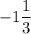
#SPJ1