Умоляю я уже не могу это решить пол дня
Только не забирайте , дайте верный ответ
1. Сторона треугольника равна 7 см, а противолежащий угол 45°. Найдите длину радиуса описанной окружности.
А) 7см; Б) см; В) 3,5 м; Г) 3,5 см.
2. Радиус окружности, вписанной в правильный треугольник, равна 4см. Найдите радиус описанной окружности.
А) 4 см; Б) 8см; В)8 см; Г) 4 см.
3. Точки А(-2;4), В(-6;12), С(2;8) являются вершинами параллелограмма АВСD. Найдите его четвертую вершину.
А) (0;6); Б) (6;0); В) (4;4); Г)(1;5).
4. Найдите координаты точки, которая симметрична точке (-2; 1) относительно начала координат.
А) (2;-1); Б) (-2;-1); В)(1;-2); Г)(-2;1).
5. Найдите косинус угла между векторами (0;-6) и ( ).
А) -1; Б) 0; В) ; Г) 2 .
Решение 6 задания должно иметь обоснование. Необходимо записать последовательные логические действия и объяснения. Правильное решение задания оценивается тремя
6. В параллелограмме острый угол равен 60°, а диагональ делит тупой угол в отношении 1:3. Вычислите периметр и большую диагональ параллелограмма, если меньшая диагональ равна 8 см.

S = 64 см²

Объяснение:

r = 4 см

= 30

S - ?

=============

Должно выполняться условие, что суммы противоположных сторон четырехугольника равны - только тогда получиться вписать в него окружность.

Распишем это условие: ⇔ 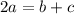. где a - боковые стороны, b и c - основы.

Сделаем вывод, что трапеция являеться равнобедренной.

Формула для нахождения площади через среднюю линию и высоту трапеции: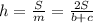 ⇔ , где S - площадь трапеции, m - средняя линия трапеции, h - ее высота. , b и c - основы трапеции.

Зная радиус вписаной окружности, мы знаем высоту трапеции: ⇔ .

Соответственно, из прямоугольного треугольника ADH1 найдём боковую сторону трапеции с соотношений: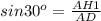 ⇒ см - боковая сторона трапеции.

Если , то зная а = 8, можем найти среднюю линию, а соответственно и площадь. 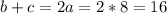см.

Просто подставляем в формулу площади: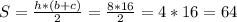 см².

находим минимум, максимум и вершину ax² + bx + c = 0  (x = -b/2a)

Функция ограничена снизу(сверху) в том случае, если она не принимает значения меньшие  (большие) некоторого числа М

М ≤ f(x)  (М ≥ f(x))

y = x² - 4x + 5,25    -1 ≤ x ≤ 4

x верш = -(-4)/2 = 2

y(2) = 4 - 8 + 5.25 = 1,25

y(-1) = (-1)² + (-1)*(-4) + 5.25 = 1 + 4 + 5.25 = 10,25

y(4) = 4² - 4*4 + 5,25 = 5.25

ограничена сверху и снизу 1.25 ≤ y ≤ 10.25

y = -x² - x + 3,75    -5 ≤ x ≤ 1

x верш = -(-1)/2(-1) = -1/2

y(-1/2) = -(-1/2)² +1/2 + 3.75 = -1/4 + 1/2 + 3.75 = 4

y(-5) = -(-5)² + (-1)*(-5) + 3.75 = -25 + 5 + 3.75 = -16,25

y(1) = -(1)² - 1*1 + 3,75 = 1.75

ограничена сверху и снизу -16.25 ≤ y ≤ 4

y = x² + 6x + 6    -6 ≤ x ≤ 0

x верш = -(6)/2 = -3

y(-3) = (-3)² + 6*(-3) + 6 = -3

y(-6) = (-6)² + 6*(-6) + 6 = 36 + -36 + 6 = 6

y(0) = 0 - 0 + 6 = 6

ограничена сверху и снизу -3 ≤ y ≤ 6